本文转载自《LDA入门与Java实现》,版权归原作者 hankcs 所有。部分内容有修改。
什么是主题模型
在我的博客上,有篇文章《基于双数组Trie树的Aho Corasick自动机极速多模式匹配》被归入算法目录,算法即为该文章的主题。而该文章因为涉及到中文分词,又被我归入了分词目录。所以该文章的主题并不单一,具体来说文中 80% 在讲算法,20% 稍微讲了下在分词中的应用。
传统的文本分类器,比如贝叶斯、kNN 和 SVM,只能将其分到一个确定的类别中。假设我给出 3 个分类“算法”“分词”“文学”让其判断,如果某个分类器将该文归入算法类,我觉得还凑合,如果分入分词,那我觉得这个分类器不够准确。
假设一个文艺小青年来看我的博客,他完全不懂算法和分词,自然也给不出具体的备选类别,有没有一种模型能够告诉这个白痴,这篇文章很可能(80%)是在讲算法,也可能(19%)是在讲分词,几乎不可能(1%)是在讲其它主题呢?
有,这样的模型就是主题模型。
什么是LDA
简述
潜在狄立克雷分配(Latent Dirichlet Allocation,LDA)主题模型是最简单的主题模型,它描述的是一篇文章是如何产生的。如图所示:
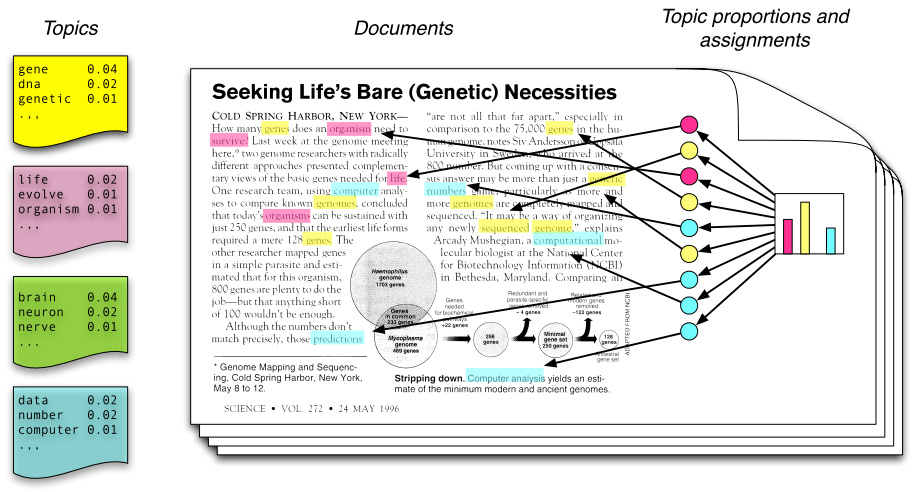
从左往右看,一个主题是由一些词语的分布定义的,比如蓝色主题是由 2% 几率的 data,2% 的 number……构成的。一篇文章则是由一些主题构成的,比如右边的直方图。具体产生过程是,从主题集合中按概率分布选取一些主题,从该主题中按概率分布选取一些词语,这些词语构成了最终的文档(LDA 模型中,词语的无序集合构成文档,也就是说词语的顺序没有关系)。
如果我们能将上述两个概率分布计算清楚,那么我们就得到了一个模型,该模型可以根据某篇文档推断出它的主题分布,即分类。由文档推断主题是文档生成过程的逆过程。
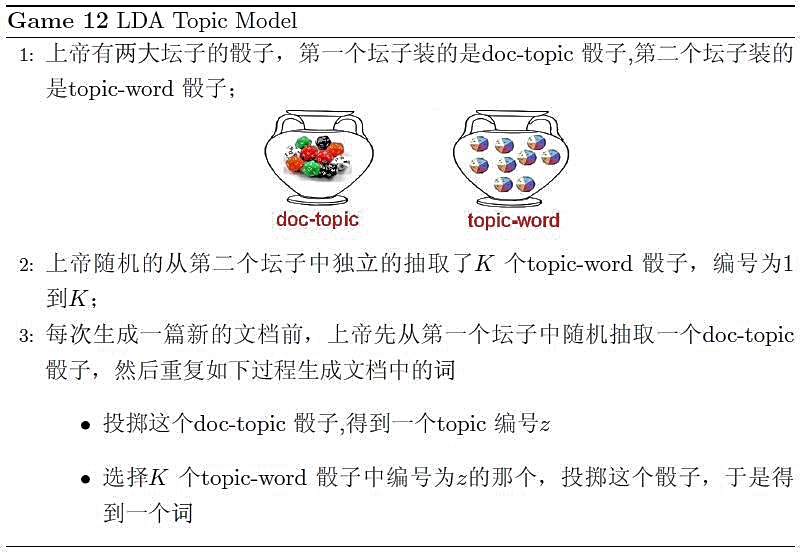
在《LDA数学八卦》一文中,对文档的生成过程有个很形象的描述:
概率模型
LDA 是一种使用联合分布来计算在给定观测变量下隐藏变量的条件分布(后验分布)的概率模型,观测变量为词的集合,隐藏变量为主题。
联合分布
LDA 的生成过程对应的观测变量和隐藏变量的联合分布如下:
\[p(\beta_{1:K},\theta_{1:D},z_{1:D},w_{1:D})=\prod_{i=1}^Kp(\beta)\prod_{d=1}^Dp(\theta_d)\Bigg(\prod_{n=1}^Np(z_{d,n}\mid\theta_d)p(w_{d,n}\mid\beta_{1:K},z_{d,n})\Bigg)\]式子有点长,耐心地从左往右看:
式子的基本符号约定——$\beta$ 表示主题,$\theta$ 表示主题的概率,$z$ 表示特定文档或词语的主题,$w$ 为词语。进一步说——
$\beta_{1:K}$ 为全体主题集合,其中 $\beta_k$ 是第k个主题的词的分布。第 $d$ 个文档中该主题所占的比例为 $\theta_d$,其中 $\theta_{d,k}$ 表示第 $k$ 个主题在第 $d$ 个文档中的比例。第 $d$ 个文档的主题全体为 $z_d$,其中 $z_{d,n}$ 是第 $d$ 个文档中第 $n$ 个词的主题。第 $d$ 个文档中所有词记为 $w_d$,其中 $w_{d,n}$ 是第 $d$ 个文档中第 $n$ 个词,每个词都是固定的词汇表中的元素。
$p(\beta)$ 表示从主题集合中选取了一个特定主题,$p(\theta_d)$ 表示该主题在特定文档中的概率,大括号的前半部分是该主题确定时该文档第 $n$ 个词的主题,后半部分是该文档第 $n$ 个词的主题与该词的联合分布。连乘符号描述了随机变量的依赖性,用概率图模型表述如下:
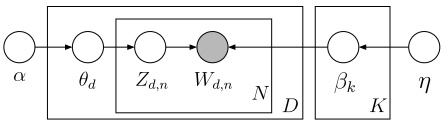
比如,先选取了主题,才能从主题里选词。具体说来,一个词受两个随机变量的影响(直接或间接),一个是确定了主题后文档中该主题的分布 $\theta_d$,另一种是第 $k$ 个主题的词的分布 $\beta_k$。
后验分布
沿用相同的符号,LDA 后验分布计算公式如下:
\[p(\beta_{1:K},\theta_{1:D},z_{1:D}\mid w_{1:D})=\frac{p(\beta_{1:K},\theta_{1:D},z_{1:D},w_{1:D})}{p(w_{1:D})}\]分子是一个联合分布,给定语料库就可以轻松统计出来。但分母无法暴力计算,因为文档集合词库达到百万(假设有 w 个词语),每个词要计算每一种可能的观测的组合(假设有 n 种组合)的概率然后累加得到先验概率,所以需要一种近似算法。
基于采样的算法通过收集后验分布的样本,以样本的分布求得后验分布的近似。
$\theta_d$ 的概率服从 Dirichlet 分布,$z_{d,n}$ 的概率服从 multinomial 分布,两个分布共轭,所谓共轭,指的就是先验分布和后验分布的形式相同:
\[Dir(\vec{p}\mid\vec{\alpha})+MultCount(\vec{m})=Dir(\vec{p}\mid\vec{\alpha}+\vec{m})\]两个分布其实是向量的分布,向量通过这两个分布取样得到。采样方法通过收集这两个分布的样本,以样本的分布近似。
马氏链和 Gibbs Sampling
这是一种统计模拟的方法。
马氏链
所谓马氏链指的是当前状态只取决于上一个状态。马氏链有一个重要的性质:状态转移矩阵 $P$ 的幂是收敛的,收敛后的转移矩阵称为马氏链的平稳分布。给定 $p(x)$,假如能够构造一个 $P$,转移 $n$ 步平稳分布恰好是 $p(x)$。那么任取一个初始状态,转移 $n$ 步之后的状态都是符合分布的样本。
Gibbs Sampling
Gibbs Sampling 是高维分布(也即类似于二维 $p(x,y)$,三维 $p(x,y,z)$ 的分布)的特化采样算法。
开源项目
参考
本文转载自《LDA入门与Java实现》,版权归原作者 hankcs 所有。部分内容有修改。