前言:概率图模型
机器学习最重要的任务,是根据一些已观察到的证据(例如训练样本)来对感兴趣的未知变量(例如类别标记)进行估计和推断。概率模型(probabilistic model)提供了一种描述框架,将学习任务归结为计算变量的概率分布。在概率模型中,利用已知变量推测未知变量的分布称为推断(inference),其核心是如何基于可观测变量推测出未知变量的条件分布。
假定所关心的变量集合为 $Y$,可观测变量集合为 $O$,其他变量的集合为 $R$。产生式模型(generative model)考虑联合分布 $P(Y,R,O)$,判别式模型(discriminative model)考虑条件分布 $P(Y,R\mid O)$。给定一组观测变量值,推断就是要由 $P(Y,R,O)$ 或 $P(Y,R\mid O)$ 得到条件概率分布 $P(Y\mid O)$。
概率图模型(probabilistic graphical model)是一类用图来表达变量相关关系的概率模型。它以图为表示工具,最常见的是用一个结点表示一个或一组随机变量,结点之间的边表示变量间的概率相关关系。概率图模型可以分为两类:第一类是使用有向无环图表示变量间的依赖关系,称为有向图模型或贝叶斯网(Bayesian network);第二类是使用无向图表示变量间的相关关系,称为无向图模型或马尔可夫网(Markov network)。
隐马尔可夫模型(Hidden Markov Model, HMM)是结构最简单的动态贝叶斯网(dynamic Bayesian network),描述由隐藏的马尔可夫链随机生成观测序列的过程,主要用于时序数据建模。在语音识别、自然语言处理等领域有广泛应用。
引入:掷骰子问题
什么是 HMM
假设我手里有三个不同的骰子:第一个骰子是我们平常见的骰子,6 个面(1,2,3,4,5,6),每个面出现的概率是 1/6,记为 D6。第二个骰子是个四面体(1,2,3,4),每个面出现的概率是 1/4,记为 D4。第三个骰子有八个面(1,2,3,4,5,6,7,8),每个面出现的概率是 1/8,记为 D8。如下图所示:
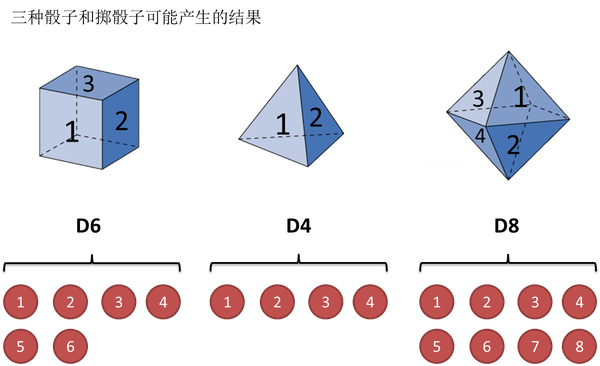
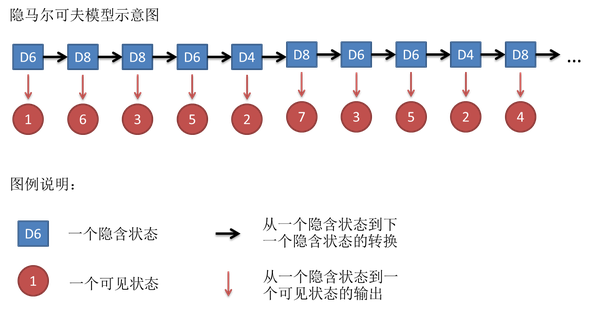
假设我们开始掷骰子,我们先从三个骰子里挑一个,挑到每一个骰子的概率都是 1/3。然后我们掷骰子,得到 1、2、3、4、5、6、7、8 中的一个数字。不停的重复上述过程,我们会得到一串数字,例如 1 6 3 5 2 7 3 5 2 4 (掷骰子 10 次)。这串数字叫做可见状态链。但是在隐马尔可夫模型中,我们不仅仅有这么一串可见状态链,还有一串隐含状态链。在这个例子里,这串隐含状态链就是你用的骰子的序列,比如:D6 D8 D8 D6 D4 D8 D6 D6 D4 D8。
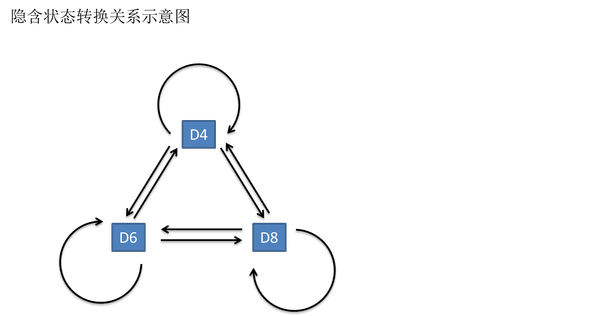
一般来说,HMM 中说到的马尔可夫链其实是指隐含状态链,因为隐含状态(骰子)之间存在转换概率(transition probability)。在我们这个例子里,D6 的下一个状态是 D4、D6、D8 的概率都是 1/3。D4、D8 下一个状态是 D4、D6、D8 的转换概率也都一样是 1/3。但是我们其实是可以随意设定转换概率的,比如,我们可以定义:D6 后面不能接 D4,D6 后面是 D6 的概率是 0.9,是 D8 的概率是 0.1,这样就是一个新的 HMM。
同样的,尽管可见状态之间没有转换概率,但是隐含状态和可见状态之间有一个概率叫做输出概率(emission probability)。就我们的例子来说,六面骰 D6 产生 1、2、3、4、5、6 的概率也都是 1/6,我们同样可以对输出概率进行其他定义。比如,我有一个被赌场动过手脚的六面骰子,掷出来是 1 的概率更大,是1/2,而掷出来是 2、3、4、5、6 的概率都是 1/10。
其实对于 HMM 来说,如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率,做模拟是相当容易的。但是应用 HMM 模型时候呢,往往是缺失了一部分信息的,有时候你知道骰子有几种,每种骰子是什么,但是不知道掷出来的骰子序列;有时候你只是看到了很多次掷骰子的结果,剩下的什么都不知道。如果应用算法去估计这些缺失的信息,就成了一个很重要的问题。
HMM 要解决的问题和解法
和 HMM 模型相关的算法主要分为三类,分别解决三种问题:
- 知道骰子有几种(隐含状态数量),每种骰子是什么(输出概率)和骰子之间的转换(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道每次掷出来的都是哪种骰子(隐含状态链)。
- 知道骰子有几种(隐含状态数量),每种骰子是什么(输出概率)和骰子之间的转换(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道掷出这个结果的概率。
- 知道骰子有几种(隐含状态数量),不知道每种骰子是什么(输出概率),也不知道骰子之间的转换(转换概率),观测到很多次掷骰子的结果(可见状态链),我想反推出每种骰子是什么(输出概率)和骰子之间的转换(转换概率)。
第 1 类问题在语音识别领域呢,叫做解码问题。这个问题其实有两种解法,会给出两个不同的答案。每个答案都对,只不过这些答案的意义不一样。第一种解法求最大似然状态路径,说通俗点呢,就是我求一串骰子序列,这串骰子序列产生观测结果的概率最大。第二种解法呢,就不是求一组骰子序列了,而是求每次掷出的骰子分别是某种骰子的概率。比如说我看到结果后,我可以求得第一次掷骰子是 D4 的概率是 0.5,D6 的概率是 0.3,D8 的概率是 0.2。第一种解法我会在下面说到。
第 2 类问题看似意义不大,因为你掷出来的结果很多时候都对应了一个比较大的概率。问这个问题的目的呢,其实是检测观察到的结果和已知的模型是否吻合。如果很多次结果都对应了比较小的概率,那么就说明我们已知的模型很有可能是错的,有人偷偷把我们的骰子給换了。
第 3 类问题很重要,因为这是最常见的情况。很多时候我们只有可见结果,不知道 HMM 模型里的参数,我们需要从可见结果估计出这些参数,这是建模的一个必要步骤。
问题阐述完了,下面就开始说解法。
1.看见不可见的,破解骰子序列
这里我说的是第一种解法,解最大似然路径问题。举例来说,我知道我有三个骰子,六面骰,四面骰,八面骰。我也知道我掷了十次的结果 (1 6 3 5 2 7 3 5 2 4),我不知道每次用了那种骰子,我想知道最有可能的骰子序列。其实最简单而暴力的方法就是穷举所有可能的骰子序列,然后把每个序列对应的概率算出来。然后我们从里面把对应最大概率的序列挑出来就行了。如果马尔可夫链不长,当然可行。如果长的话,穷举的数量太大,就很难完成了。
另外一种很有名的算法叫做 Viterbi algorithm,要理解这个算法,我们先看几个简单的列子。
首先,如果我们只掷一次骰子:

看到结果为 (1),我们需要计算第一个骰子是 D6、D4、D8 的最大概率。第一个骰子是 D6 的最大概率为 $P1(D6) = P(D6)P(D6\rightarrow1)=\frac{1}{3}*\frac{1}{6}=\frac{1}{18}$,同样我们可以计算 $P1(D4)=\frac{1}{3}*\frac{1}{4}=\frac{1}{12}$、$P1(D8)=\frac{1}{3}*\frac{1}{8}=\frac{1}{24}$。对应的最大概率骰子序列就是 D4。把这个
情况拓展,我们掷两次骰子:

结果为 (1,6),同样的,我们要计算第二个骰子是 D6、D4、D8 的最大概率。第二个骰子取到 D6 的最大概率是:
\[\begin{align}P2(D6) &= \max\begin{pmatrix} P1(D6)P(D6\rightarrow D6)\\P1(D4)P(D4\rightarrow D6)\\P1(D8)P(D8\rightarrow D6)\end{pmatrix}P(D6\rightarrow6)\\&=P1(D4)P(D4\rightarrow D6)P(D6\rightarrow 6)=\frac{1}{12}*\frac{1}{3}*\frac{1}{6}=\frac{1}{216}\end{align}\]同理我们可以计算出第二个骰子是 D4 或 D8 时的最大概率 $P2(D4)=\frac{1}{12}*\frac{1}{3}*0=0$、$P2(D8)=\frac{1}{12}*\frac{1}{3}*\frac{1}{8}=\frac{1}{288}$。我们发现,第二个骰子取到 D6 的概率最大而使,这个概率最大时,第一个骰子为 D4。所以最大概率骰子序列就是 (D4 D6)。
继续拓展,我们掷三次骰子:

同样,我们计算第三个骰子分别是 D6、D4、D8 的最大概率。第三个骰子取到 D6 的最大概率是:
\[\begin{align}P3(D6)&=\max\begin{pmatrix}P2(D4)P(D4\rightarrow D6)\\P2(D6)P(D6\rightarrow D6)\\P2(D8)P(D8\rightarrow D6)\end{pmatrix}P(D6\rightarrow 3)\\&=P2(D6)P(D6\rightarrow D6)P(D6\rightarrow 3)=\frac{1}{216}*\frac{1}{3}*\frac{1}{6}=\frac{1}{3888}\end{align}\]同理,我们可以计算出第三个骰子是 D4、D8 的最大概率 $P3(D4)=\frac{1}{216}*\frac{1}{3}*\frac{1}{4}=\frac{1}{2592}$、$P3(D8)=\frac{1}{216}*\frac{1}{3}*\frac{1}{8}=\frac{1}{5184}$。我们发现,第三个骰子取到 D4 的概率最大。而使这个概率最大时,第二个骰子为 D6,第一个骰子为 D4,所以最大概率骰子序列就是 (D4 D6 D4)。
既然掷骰子一二三次可以算,掷多少次都可以以此类推。我们发现,我们要求最大概率骰子序列时要做这么几件事情。首先,不管序列多长,要从序列长度为 1 算起,算序列长度为 1 时取到每个骰子的最大概率。然后,逐渐增加长度,每增加一次长度,重新算一遍在这个长度下最后一个位置取到每个骰子的最大概率。因为上一个长度下的取到每个骰子的最大概率都算过了,重新计算的话其实不难。当我们算到最后一位时,就知道最后一位是哪个骰子的概率最大了。然后,我们要把对应这个最大概率的序列从后往前推出来。
2.谁动了我的骰子?
比如说你怀疑自己的六面骰被赌场动过手脚了,有可能被换成另一种六面骰,这种六面骰掷出来是 1 的概率更大,是 1/2,而掷出来是 2、3、4、5、6 的概率都是 1/10。你怎么办么?答案很简单,算一算正常的三个骰子掷出一段序列的概率,再算一算不正常的六面骰和另外两个正常骰子掷出这段序列的概率。如果前者比后者小,你就要小心了。
比如说掷骰子的结果是:

要算用正常的三个骰子掷出这个结果的概率,其实就是将所有可能情况的概率进行加和计算。同样,简单而暴力的方法就是把穷举所有的骰子序列,还是计算每个骰子序列对应的概率,但是这回,我们不挑最大值了,而是把所有算出来的概率相加,得到的总概率就是我们要求的结果。这个方法依然不能应用于太长的骰子序列(马尔可夫链)。
我们会应用一个和前一个问题类似的解法,只不过前一个问题关心的是概率最大值,这个问题关心的是概率之和。解决这个问题的算法叫做前向算法(forward algorithm)。
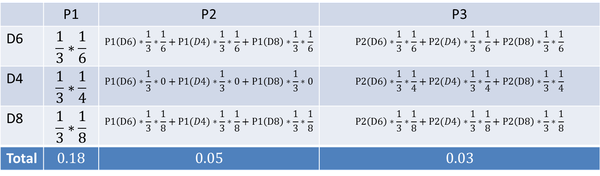
首先,如果我们只掷一次骰子:

看到结果为 (1),产生这个结果的总概率可以按照如下计算,总概率为 0.18:

把这个情况拓展,我们掷两次骰子:

看到结果为 (1 6),产生这个结果的总概率可以按照如下计算,总概率为 0.05:

继续拓展,我们掷三次骰子:

看到结果为 (1 6 3),产生这个结果的总概率可以按照如下计算,总概率为 0.03:
同样的,我们一步一步的算,有多长算多长,再长的马尔可夫链总能算出来的。用同样的方法,也可以算出不正常的六面骰和另外两个正常骰子掷出这段序列的概率,然后我们比较一下这两个概率大小,就能知道你的骰子是不是被人换了。
3.掷一串骰子出来,让我猜猜你是谁
这块暂时还没写,使用一个号称 EM 的算法。
参考
- 周志华《机器学习》
- 李航《统计学习方法》
- Yang Eninala 在如何用简单易懂的例子解释隐马尔可夫模型?的回答