浅谈 NLP 中的 Attention 机制

（本文于 2020 年 6 月 14 日更新）

如今 NLP 领域，Attention 大行其道，当然也不止 NLP，在 CV 领域 Attention 也占有一席之地（Non Local、SAGAN 等）。众多 NLP&CV 的成果已经充分肯定了 Attention 的有效性。

背景

2017 年中，有两篇类似并且都算是 Seq2Seq 上的创新的论文，分别是 FaceBook 的《Convolutional Sequence to Sequence Learning》和 Google 的《Attention is All You Need》。本质上来说，它们都是抛弃了 RNN 结构来做 Seq2Seq 任务。

本文将首先对《Attention is All You Need》做一点简单的分析，然后再介绍一些 Attention 的变体。

序列编码

深度学习做 NLP 的方法，基本上都是先将句子分词，然后每个词转化为对应的词向量序列。这样一来，每个句子都对应的是一个矩阵 $\boldsymbol{X}=(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n)$，其中 $\boldsymbol{x}_i$ 代表着第 $i$ 个词的词向量（行向量），维度为 $d$ 维，故 $\boldsymbol{X}\in \mathbb{R}^{n\times d}$。这样的话，问题就变成了编码这些序列了。

第一个基本的思路是 RNN 层，RNN 的方案很简单，递归式进行：

不管是已经被广泛使用的 LSTM、GRU 还是最近的 SRU，都并未脱离这个递归框架。RNN 结构本身比较简单，也很适合序列建模，但 RNN 的明显缺点之一就是无法并行，因此速度较慢，这是递归的天然缺陷。另外我个人觉得 RNN 无法很好地学习到全局的结构信息，因为它本质是一个马尔科夫决策过程。

第二个思路是 CNN 层，其实 CNN 的方案也是很自然的，窗口式遍历，比如尺寸为 3 的卷积，就是

在 FaceBook 的论文中，纯粹使用卷积也完成了 Seq2Seq 的学习，是卷积的一个精致且极致的使用案例，热衷卷积的读者必须得好好读读这篇文论。CNN 方便并行，而且容易捕捉到一些全局的结构信息，在目前的工作或竞赛模型中，我都已经尽量用 CNN 来代替已有的 RNN 模型了。

Google 的大作提供了第三个思路：纯 Attention！单靠注意力就可以！RNN 要逐步递归才能获得全局信息，因此一般要双向 RNN 才比较好；CNN 事实上只能获取局部信息，是通过层叠来增大感受野；Attention 的思路最为粗暴，它一步到位获取了全局信息！它的解决方案是：

其中 $\boldsymbol{A},\boldsymbol{B}$ 是另外一个序列（矩阵）。如果都取 $\boldsymbol{A}=\boldsymbol{B}=\boldsymbol{X}$，那么就称为 Self Attention，它的意思是直接将 $\boldsymbol{x}_t$ 与原来的每个词进行比较，最后算出 $\boldsymbol{y}_t$！

Attention

Attention 定义

Google 的一般化 Attention 思路也是一个编码序列的方案，因此我们也可以认为它跟 RNN、CNN 一样，都是一个序列编码的层。

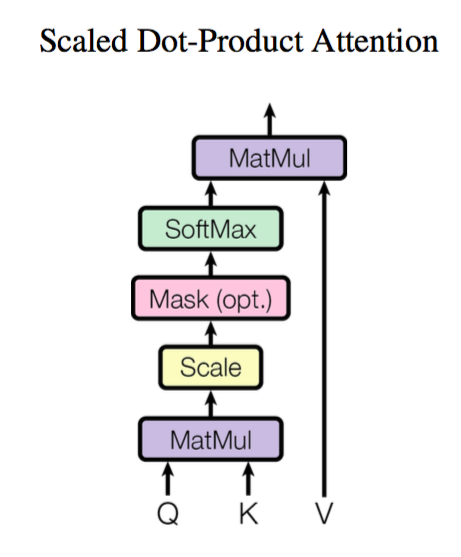
前面给出的是一般化的框架形式的描述，事实上 Google 给出的方案是很具体的。首先，它先把 Attention 的定义给了出来：

其中 $\boldsymbol{Q}\in\mathbb{R}^{n\times d_k}, \boldsymbol{K}\in\mathbb{R}^{m\times d_k}, \boldsymbol{V}\in\mathbb{R}^{m\times d_v}$。那怎么理解这种结构呢？我们不妨逐个向量来看。

其中 $Z$ 是归一化因子。事实上 $q,k,v$ 分别是 $query,key,value$ 的简写，$K,V$ 是一一对应的，它们就像是 key-value 的关系，那么上式的意思就是通过 $\boldsymbol{q}_t$ 这个 query，通过与各个 $\boldsymbol{k}_s$ 的内积并 softmax 的方式，来得到 $\boldsymbol{q}_t$ 与各个 $\boldsymbol{v}_s$ 的相似度，然后加权求和，得到一个 $d_v$ 维的向量。其中因子 $\sqrt{d_k}$ 起到调节作用，使得内积不至于太大（太大的话 softmax 后就非 0 即 1 了，不够“soft”了）。

事实上这种 Attention 的定义并不新鲜，但由于 Google 的影响力，我们可以认为现在是更加正式地提出了这个定义，并将其视为一个层地看待；此外这个定义只是注意力的一种形式，还有一些其他选择，比如 $query$ 跟 $key$ 的运算方式不一定是点乘（还可以是拼接后再内积一个参数向量），甚至权重都不一定要归一化，等等。

Multi-Head Attention

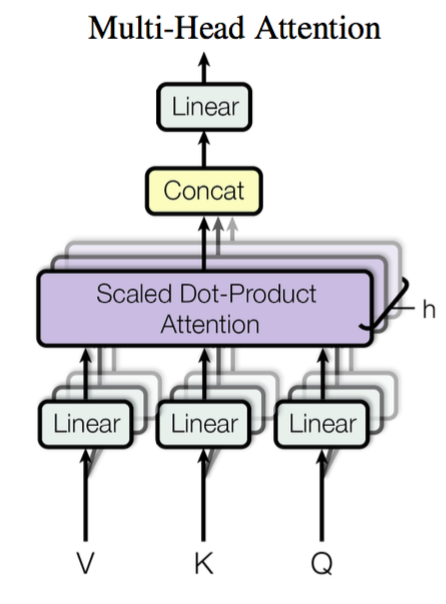
这个是 Google 提出的新概念，是 Attention 机制的完善。不过从形式上看，它其实就再简单不过了，就是把 $\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$ 通过参数矩阵映射一下，然后再做 Attention，把这个过程重复做 $h$ 次，结果拼接起来就行了，可谓“大道至简”了。具体来说

这里 $\boldsymbol{W}_i^Q\in\mathbb{R}^{d_k\times \tilde{d}_k}, \boldsymbol{W}_i^K\in\mathbb{R}^{d_k\times \tilde{d}_k}, \boldsymbol{W}_i^V\in\mathbb{R}^{d_v\times \tilde{d}_v}$，然后

最后得到一个 $n\times (h\tilde{d}_v)$ 的序列。所谓“多头”（Multi-Head），就是只多做几次同样的事情（参数不共享），然后把结果拼接。

Self Attention

到目前为止，对 Attention 层的描述都是一般化的，我们可以落实一些应用。比如，如果做阅读理解的话，$\boldsymbol{Q}$ 可以是篇章的词向量序列，取 $\boldsymbol{K}=\boldsymbol{V}$ 为问题的词向量序列，那么输出就是所谓的 Aligned Question Embedding。

而在 Google 的论文中，大部分的 Attention 都是 Self Attention，即“自注意力”。所谓 Self Attention，其实就是 $Attention(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})$，$\boldsymbol{X}$ 就是前面说的输入序列。也就是说，在序列内部做 Attention，寻找序列内部的联系。

Google 论文的主要贡献之一是它表明了内部注意力在机器翻译（甚至是一般的 Seq2Seq 任务）的序列编码上是相当重要的，而之前关于 Seq2Seq 的研究基本都只是把注意力机制用在解码端。类似的事情是，目前 SQUAD 阅读理解的榜首模型 R-Net 也加入了自注意力机制，这也使得它的模型有所提升。

当然，更准确来说，Google 所用的是 Self Multi-Head Attention：

Position Embedding

然而，只要稍微思考一下就会发现，这样的模型并不能捕捉序列的顺序！换句话说，如果将 $\boldsymbol{K},\boldsymbol{V}$ 按行打乱顺序（相当于句子中的词序打乱），那么 Attention 的结果还是一样的。这就表明了，到目前为止，Attention 模型顶多是一个非常精妙的“词袋模型”而已。

这问题就比较严重了，大家知道，对于时间序列来说，尤其是对于 NLP 中的任务来说，顺序是很重要的信息，它代表着局部甚至是全局的结构，学习不到顺序信息，那么效果将会大打折扣（比如机器翻译中，有可能只把每个词都翻译出来了，但是不能组织成合理的句子）。

于是 Google 再祭出了一招——Position Embedding，也就是“位置向量”，将每个位置编号，然后每个编号对应一个向量，通过结合位置向量和词向量，就给每个词都引入了一定的位置信息，这样 Attention 就可以分辨出不同位置的词了。

Position Embedding 并不算新鲜的玩意，在 FaceBook 的《Convolutional Sequence to Sequence Learning》也用到了这个东西。但在 Google 的这个作品中，它的 Position Embedding 有几点区别：

• 以前在 RNN、CNN 模型中其实都出现过 Position Embedding，但在那些模型中，Position Embedding 是锦上添花的辅助手段，也就是“有它会更好、没它也就差一点点”的情况，因为 RNN、CNN 本身就能捕捉到位置信息。但是在这个纯 Attention 模型中，Position Embedding 是位置信息的唯一来源，因此它是模型的核心成分之一，并非仅仅是简单的辅助手段。

• 在以往的 Position Embedding 中，基本都是根据任务训练出来的向量。而 Google 直接给出了一个构造 Position Embedding 的公式： \(\left\{\begin{aligned}&PE_{2i}(p)=\sin\Big(p/10000^{2i/{d_{pos}}}\Big)\\ &PE_{2i+1}(p)=\cos\Big(p/10000^{2i/{d_{pos}}}\Big) \end{aligned}\right.\) 这里的意思是将 id 为 $p$ 的位置映射为一个 $d_{pos}$ 维的位置向量，这个向量的第 $i$ 个元素的数值就是 $PE_i(p)$。Google 在论文中说到他们比较过直接训练出来的位置向量和上述公式计算出来的位置向量，效果是接近的。因此显然我们更乐意使用公式构造的 Position Embedding 了。

• Position Embedding 本身是一个绝对位置的信息，但在语言中，相对位置也很重要，Google选择前述的位置向量公式的一个重要原因是：由于我们有 $\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$ 以及 $\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$，这表明位置 $p+k$ 的向量可以表明位置 $p$ 的向量的线性变换，这提供了表达相对位置信息的可能性。

结合位置向量和词向量有几个可选方案，可以把它们拼接起来作为一个新向量，也可以把位置向量定义为跟词向量一样大小，然后两者加起来。FaceBook 的论文和 Google 论文中用的都是后者。直觉上相加会导致信息损失，似乎不可取，但 Google 的成果说明相加也是很好的方案。

稀疏 Attention

从前面的介绍可以看到，Attention 的计算量并不低。比如 Self Attention 包含了两次序列自身的矩阵乘法，这两次矩阵乘法的计算量都是 $\mathscr{O}(n^2)$ 的，要是序列足够长，这个计算量其实是很难接受的。而且并非所有问题都需要长程的、全局的依赖的，也有很多问题只依赖于局部结构，这时候用纯 Attention 也不大好。

从理论上来讲，Self Attention 的计算时间和显存占用量都是 $\mathscr{O}(n^2)$ 级别的（$n$ 是序列长度），这就意味着如果序列长度变成原来的 2 倍，显存占用量就是原来的 4 倍，计算时间也是原来的 4 倍。当然，假设并行核心数足够多的情况下，计算时间未必会增加到原来的 4 倍，但是显存的 4 倍却是实实在在的，无可避免，这也是微调 Bert 的时候时不时就来个 OOM 的原因了。

我们说 Self Attention 是 $\mathscr{O}(n^2)$ 的，那是因为它要对序列中的任意两个向量都要计算相关度，得到一个 $n^2$ 大小的相关度矩阵：

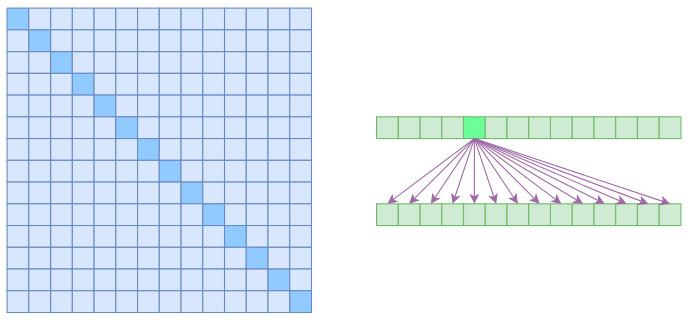
在上图中，左边显示了注意力矩阵，右变显示了关联性，这表明每个元素都跟序列内所有元素有关联。

所以，如果要节省显存，加快计算速度，那么一个基本的思路就是减少关联性的计算，也就是认为每个元素只跟序列内的一部分元素相关，这就是稀疏 Attention 的基本原理。

稀疏 Attention 源于 OpenAI 的论文《Generating Long Sequences with Sparse Transformers》。

下面我们将会介绍 Attention 的一些变体，这些变体的共同特点是——“为节约而生”——既节约时间，也节约显存。

Atrous Self Attention

第一个要引入的概念是 Atrous Self Attention，中文可以称之为“膨胀自注意力”、“空洞自注意力”、“带孔自注意力”等。这个名称跟后面的 Local Self Attention 一样，都是笔者根据它的特性自行命名的，原论文《Generating Long Sequences with Sparse Transformers》并没有出现过这两个概念，但我认为将它们单独引出来是有意义的。

很显然，Atrous Self Attention 就是启发于“膨胀卷积（Atrous Convolution）”，如下右图所示，它对相关性进行了约束，强行要求每个元素只跟它相对距离为 $k,2k,3k,\dots$ 的元素关联，其中 $k > 1$ 是预先设定的超参数。从下左的注意力矩阵看，就是强行要求相对距离不是 $k$ 的倍数的注意力为 0（白色代表 0）：

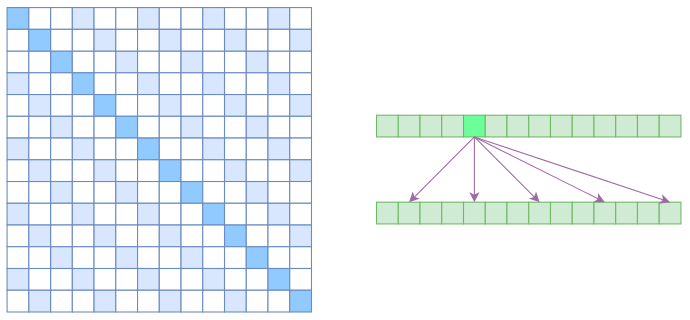
由于现在计算注意力是“跳着”来了，所以实际上每个元素只跟大约 $n/k$ 个元素算相关性，这样一来理想情况下运行效率和显存占用都变成了 $\mathscr{O}(n^2/k)$，也就是说能直接降低到原来的 $1/k$。

Local Self Attention

另一个要引入的过渡概念是 Local Self Attention，中文可称之为“局部自注意力”。其实自注意力机制在 CV 领域统称为“Non Local”，而显然 Local Self Attention 则要放弃全局关联，重新引入局部关联。具体来说也很简单，就是约束每个元素只与前后 $k$ 个元素以及自身有关联，如下图所示：

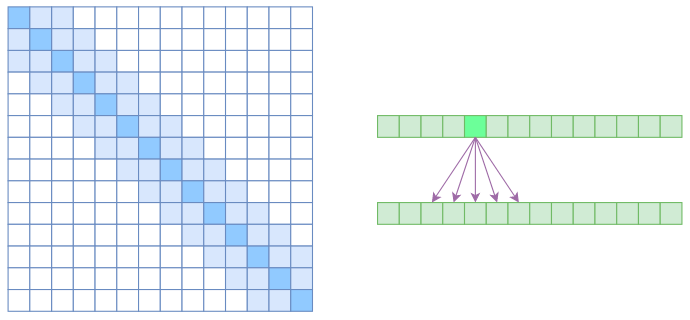
从注意力矩阵来看，就是相对距离超过 $k$ 的注意力都直接设为 0。

其实 Local Self Attention 就跟普通卷积很像了，都是保留了一个 $2k+1$ 大小的窗口，然后在窗口内进行一些运算，不同的是普通卷积是把窗口展平然后接一个全连接层得到输出，而现在是窗口内通过注意力来加权平均得到输出。对于 Local Self Attention 来说，每个元素只跟 $2k+1$ 个元素算相关性，这样一来理想情况下运行效率和显存占用都变成了 $\mathscr{O}((2k+1)n)\sim \mathscr{O}(kn)$ 了，也就是说随着 $n$ 而线性增长，这是一个很理想的性质——当然也直接牺牲了长程关联性。

Sparse Self Attention

到此，就可以很自然地引入 OpenAI 的 Sparse Self Attention 了。我们留意到，Atrous Self Attention 是带有一些洞的，而 Local Self Attention 正好填补了这些洞，所以一个简单的方式就是将 Local Self Attention 和 Atrous Self Attention 交替使用，两者累积起来，理论上也可以学习到全局关联性，也省了显存。

简单画个草图就可以知道，假如第一层用 Local Self Attention 的话，那么输出的每个向量都融合了局部的几个输入向量，然后第二层用 Atrous Self Attention，虽然它是跳着来，但是因为第一层的输出融合了局部的输入向量，所以第二层的输出理论上可以跟任意的输入向量相关，也就是说实现了长程关联。

但是 OpenAI 没有这样做，它直接将两个 Atrous Self Attention 和 Local Self Attention 合并为一个，如下图：

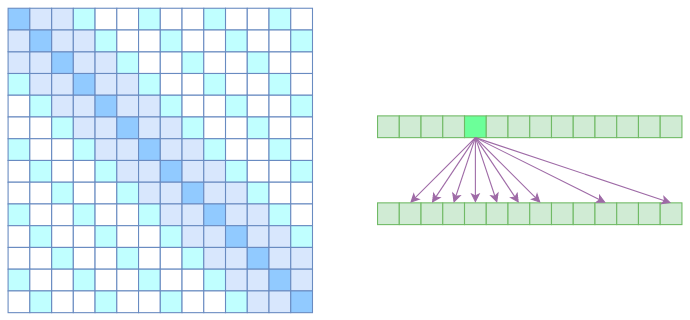
从注意力矩阵上看就很容易理解了，就是除了相对距离不超过 $k$ 的、相对距离为 $k,2k,3k,\dots$ 的注意力都设为 0，这样一来 Attention 就具有“局部紧密相关和远程稀疏相关”的特性，这对很多任务来说可能是一个不错的先验，因为真正需要密集的长程关联的任务事实上是很少的。

代码实现

最后，为了使得本文有点实用价值，笔者试着给出了以上各种 Attention 的实现代码。

注意的是，Multi-Head 的意思虽然很简单——重复做几次然后拼接，但事实上不能按照这个思路来写程序，这样会非常慢。因为 tensorflow 是不会自动并行的，比如

a = tf.zeros((10, 10))
b = a + 1
c = a + 2

其中 b,c 的计算是串联的，尽管 b、c 没有相互依赖。因此我们必须把 Multi-Head 的操作合并到一个张量来运算，因为单个张量的乘法内部则会自动并行。

此外，我们要对序列做 Mask 以忽略填充部分的影响。一般的 Mask 是将填充部分置零，但 Attention 中的 Mask 是要在 softmax 之前，把填充部分减去一个大整数（这样 softmax 之后就非常接近 0 了）。这些内容都在代码中有对应的实现。

上面的 Atrous Self Attention、Local Self Attention、Sparse Self Attention 都算是稀疏 Attention，直观上来看就是注意力矩阵变得很稀疏了。那怎么实现它们呢？如果直接在注意力矩阵中对为零的部分进行 mask 的话，那在数学上（功能上）是没有问题的，但这样做并不能提速，也不能省显存。

官方实现

OpenAI 也开源了自己的实现，位于：https://github.com/openai/sparse_attention

这是基于 tensorflow 的，还用到了它们自己的一个稀疏矩阵库 blocksparse。不过这玩意似乎封装得很奇怪，我不知道怎么将它迁移到 Keras，而且它用了很多 Python 3 的特性，不能直接用于 Python 2。如果用 Python 3 和纯 Tensorflow 的朋友可以试试。

还有一个问题是 OpenAI 原论文主要是用稀疏 Attention 来生成超长序列，所以它在论文中和代码中都把注意力矩阵的所有上三角部分都 mask了（避免用到未来信息），但未必所有用到稀疏 Attention 的都是生成场景，而且对于基本概念的介绍来说，这是不必要的，这也是笔者不按原论文的思路来介绍的原因之一。

Keras 实现

对于 Keras，笔者根据自己构思的写法实现了基础 Attention 以及三种稀疏 Attention： https://github.com/bojone/attention/blob/master/attention_keras.py

经过实验，发现在笔者的写法中，这三种稀疏 Attention 相比全量 Attention 确实能节省一些内存，但遗憾的是，除了 Atrous Self Attention 外，剩下两种 Attention 的实现都不能提速，反而降低了一点速度，这是因为实现过程中没有充分利用稀疏性所致的，而 OpenAI 的 blocksparse 则是经过高度优化，而且是直接写的 CUDA 代码，这没法比。但不管速度如何，三种稀疏 Attention 功能上应该是没毛病的。

代码测试

在 Keras 上对 IMDB 进行简单的测试：

#coding:utf-8

from attention_keras import SelfAttention, SinCosPositionEmbedding
from keras.preprocessing import sequence
from keras.datasets import imdb
from keras.models import Model
from keras.layers import *
import keras.backend as K 

max_features = 20000
maxlen = 100
batch_size = 32

print('Loading data...')
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=max_features)
print(len(x_train), 'train sequences')
print(len(x_test), 'test sequences')

print('Pad sequences (samples x time)')
x_train = sequence.pad_sequences(x_train, maxlen=maxlen)
x_test = sequence.pad_sequences(x_test, maxlen=maxlen)
print('x_train shape:', x_train.shape)
print('x_test shape:', x_test.shape)

S_inputs = Input(shape=(None,), dtype='int32')
S_mask = Lambda(lambda x: K.cast(K.greater(K.expand_dims(x, 2), 0), 'float32'))(S_inputs)
embeddings = Embedding(max_features, 128)(S_inputs)
# embeddings = SinCosPositionEmbedding(128, merge_mode='concate')(embeddings)

O_seq = SelfAttention(8,16)([embeddings,S_mask])
O_seq = GlobalAveragePooling1D()(O_seq)
O_seq = Dropout(0.5)(O_seq)
outputs = Dense(1, activation='sigmoid')(O_seq)

model = Model(inputs=S_inputs, outputs=outputs)

model.compile(loss='binary_crossentropy',
              optimizer='adam',
              metrics=['accuracy'])

print('Train...')
model.fit(x_train, y_train,
          batch_size=batch_size,
          epochs=10,
          validation_data=(x_test, y_test))

无 Position Embedding 的结果：

Train on 25000 samples, validate on 25000 samples
Epoch 1/10
25000/25000 [==============================] - 15s 617us/step - loss: 0.3944 - acc: 0.8192 - val_loss: 0.3408 - val_acc: 0.8493
Epoch 2/10
25000/25000 [==============================] - 6s 253us/step - loss: 0.2370 - acc: 0.9040 - val_loss: 0.3735 - val_acc: 0.8404
Epoch 3/10
25000/25000 [==============================] - 6s 260us/step - loss: 0.1779 - acc: 0.9316 - val_loss: 0.4397 - val_acc: 0.8310
Epoch 4/10
25000/25000 [==============================] - 6s 253us/step - loss: 0.2512 - acc: 0.8964 - val_loss: 0.4357 - val_acc: 0.8084
Epoch 5/10
25000/25000 [==============================] - 7s 262us/step - loss: 0.2644 - acc: 0.8898 - val_loss: 0.4675 - val_acc: 0.8039
Epoch 6/10
25000/25000 [==============================] - 6s 248us/step - loss: 0.2224 - acc: 0.9088 - val_loss: 0.5348 - val_acc: 0.8016
Epoch 7/10
25000/25000 [==============================] - 6s 245us/step - loss: 0.2026 - acc: 0.9201 - val_loss: 0.5366 - val_acc: 0.7985
Epoch 8/10
25000/25000 [==============================] - 6s 255us/step - loss: 0.1929 - acc: 0.9222 - val_loss: 0.5839 - val_acc: 0.7930
Epoch 9/10
25000/25000 [==============================] - 7s 267us/step - loss: 0.1800 - acc: 0.9280 - val_loss: 0.6316 - val_acc: 0.7881
Epoch 10/10
25000/25000 [==============================] - 7s 270us/step - loss: 0.1714 - acc: 0.9317 - val_loss: 0.6585 - val_acc: 0.7878

有 Position Embedding 的结构：

Train on 25000 samples, validate on 25000 samples
Epoch 1/10
25000/25000 [==============================] - 15s 610us/step - loss: 0.5646 - acc: 0.7453 - val_loss: 0.5143 - val_acc: 0.7626
Epoch 2/10
25000/25000 [==============================] - 7s 287us/step - loss: 0.4609 - acc: 0.7976 - val_loss: 0.4304 - val_acc: 0.8097
Epoch 3/10
25000/25000 [==============================] - 7s 283us/step - loss: 0.4078 - acc: 0.8253 - val_loss: 0.4278 - val_acc: 0.8148
Epoch 4/10
25000/25000 [==============================] - 7s 280us/step - loss: 0.3797 - acc: 0.8373 - val_loss: 0.3997 - val_acc: 0.8231
Epoch 5/10
25000/25000 [==============================] - 7s 280us/step - loss: 0.3397 - acc: 0.8591 - val_loss: 0.3931 - val_acc: 0.8306
Epoch 6/10
25000/25000 [==============================] - 7s 264us/step - loss: 0.3027 - acc: 0.8748 - val_loss: 0.3893 - val_acc: 0.8313
Epoch 7/10
25000/25000 [==============================] - 8s 300us/step - loss: 0.2759 - acc: 0.8889 - val_loss: 0.3931 - val_acc: 0.8306
Epoch 8/10
25000/25000 [==============================] - 7s 296us/step - loss: 0.2468 - acc: 0.9006 - val_loss: 0.4125 - val_acc: 0.8267
Epoch 9/10
25000/25000 [==============================] - 7s 292us/step - loss: 0.2229 - acc: 0.9121 - val_loss: 0.4473 - val_acc: 0.8182
Epoch 10/10
25000/25000 [==============================] - 7s 284us/step - loss: 0.2012 - acc: 0.9223 - val_loss: 0.4871 - val_acc: 0.8118

貌似最高准确率比单层的 LSTM 准确率还高一点，另外还可以看到 Position Embedding 能减弱过拟合。

我们真的了解自注意力吗？

直观上来看，自注意力机制算是解释性比较强的模型之一了，它通过自己与自己的 Attention 来自动捕捉了 token 与 token 之间的关联，事实上在《Attention is All You Need》那篇论文中，就给出了如下的看上去挺合理的可视化效果：

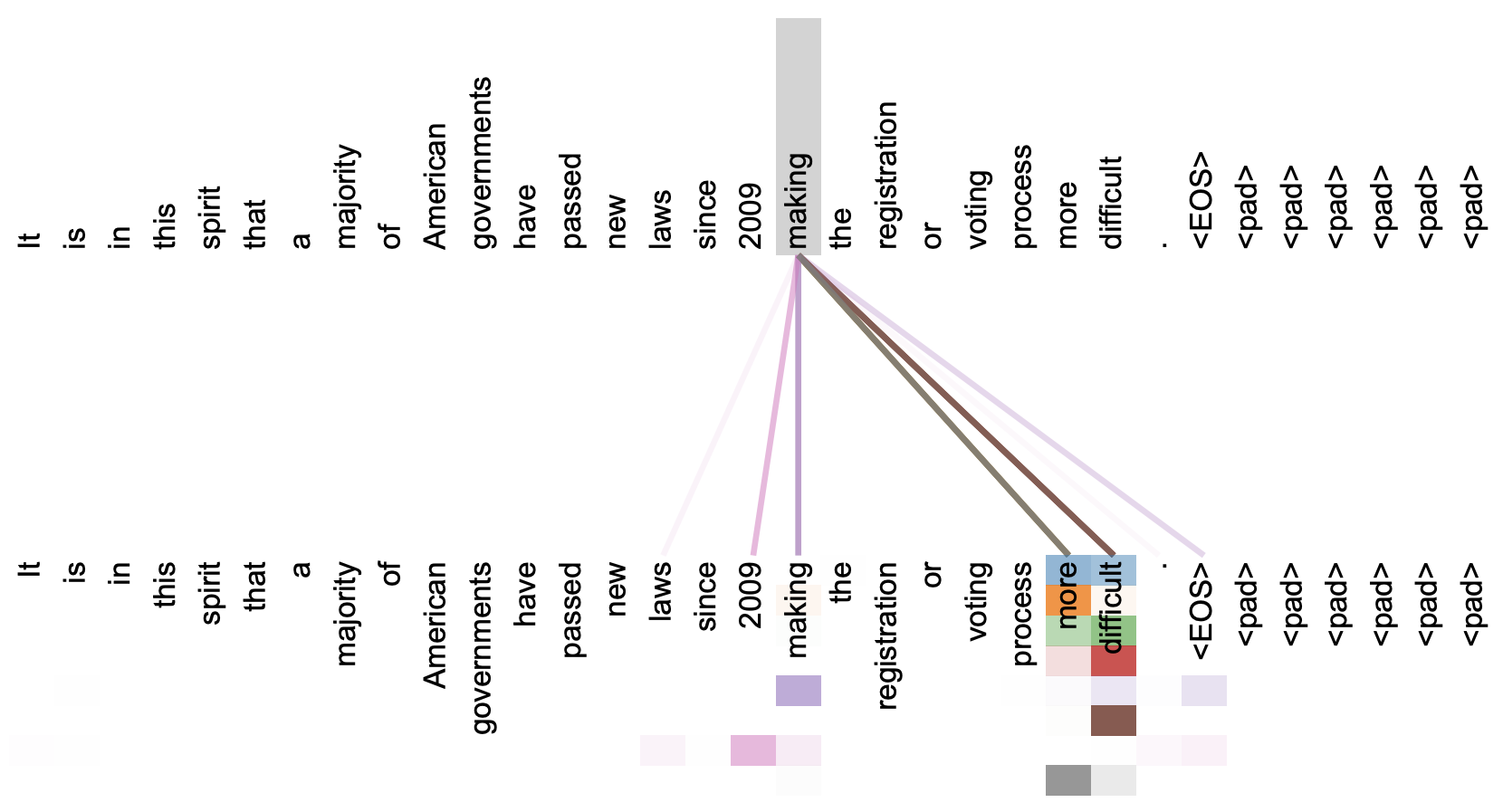
但自注意力机制真的是这样生效的吗？这种”token 对 token“的注意力是必须的吗？2020 年 Google 的新论文《Synthesizer: Rethinking Self-Attention in Transformer Models》对自注意力机制做了一些“异想天开”的探索，结果也许会颠覆我们对自注意力的认知。

天马行空

正如前文所说，自注意力就是对于同一个 $\boldsymbol{X}\in \mathbb{R}^{n\times d}$，通过不同的投影矩阵 $\boldsymbol{W}_q,\boldsymbol{W}_k,\boldsymbol{W}_v\in\mathbb{R}^{d\times d’}$ 得到 $\boldsymbol{Q}=\boldsymbol{X}\boldsymbol{W}_q,\boldsymbol{K}=\boldsymbol{X}\boldsymbol{W}_k,\boldsymbol{V}=\boldsymbol{X}\boldsymbol{W}_v$，然后再做 Attention，即

Multi-Head Attention 类似，则不过是 Attention 运算在不同的参数下重复多次然后将多个输出拼接起来，属于比较朴素的增强。

从本质上来看，自注意力就是通过一个 $n\times n$ 的矩阵 $\boldsymbol{A}$ 和 $d\times d’$ 的矩阵 $\boldsymbol{W}_v$，将原本是 $n\times d$ 的矩阵 $\boldsymbol{X}$，变成了 $n\times d’$ 的矩阵 $\boldsymbol{A}\boldsymbol{X}\boldsymbol{W}_v$。其中矩阵 $\boldsymbol{A}$ 是动态生成的，即

对于矩阵 $\boldsymbol{B}$，本质上来说它就是 $\boldsymbol{X}$ 里边两两向量的内积组合，所以我们称它为“token 对 token”的 Attention。

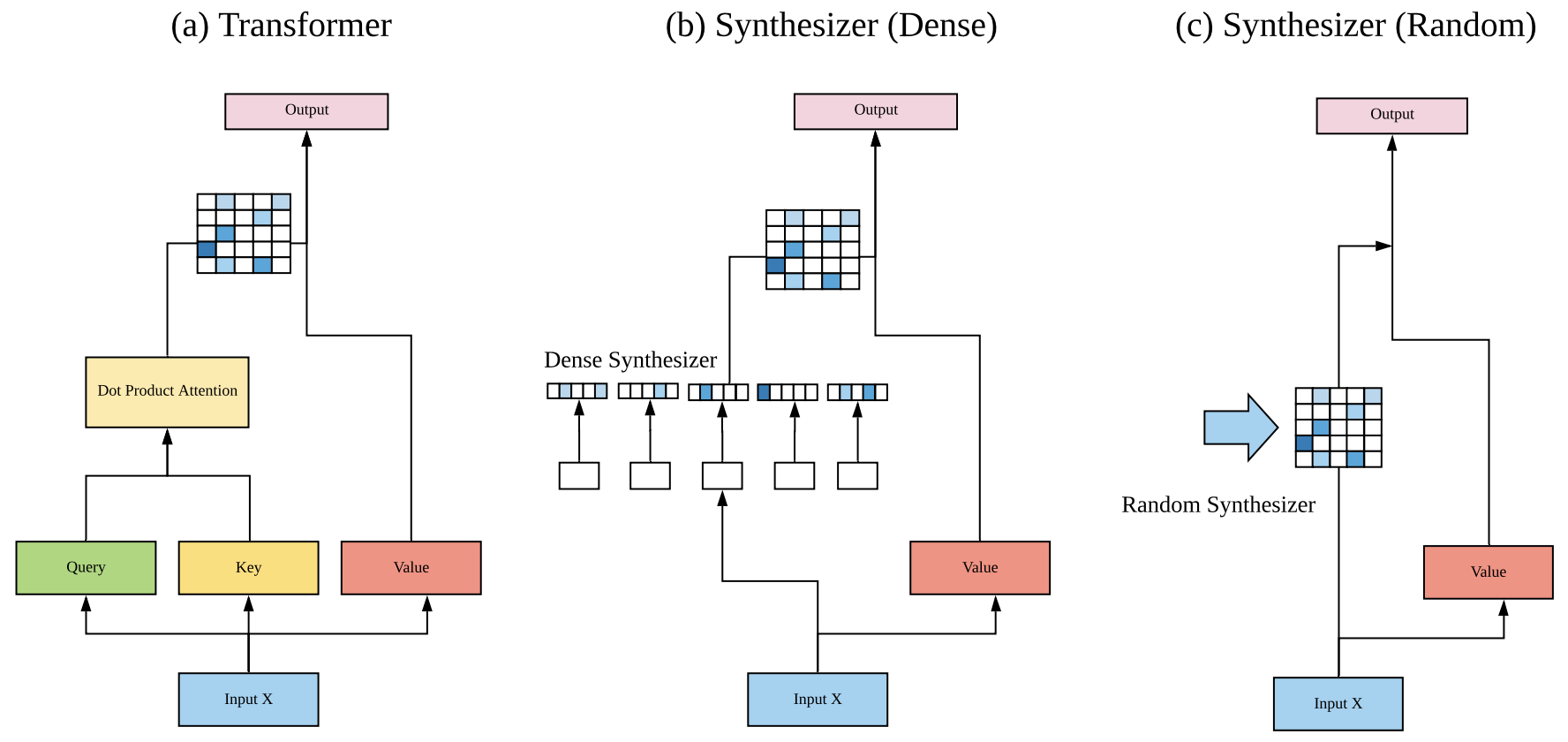
那么，就到了前面提出的问题：“token 对 token”是必须的吗？能不能通过其他方式来生成这个矩阵 $\boldsymbol{B}$？Google 的这篇论文正是“天马行空”了几种新的形式并做了实验，这些形式统称为 Synthesizer。

Dense 形式

第一种形式在原论文中称为 $\text{Dense}$：$\boldsymbol{B}$ 需要是 $n\times n$ 大小的，而 $\boldsymbol{X}$ 是 $n\times d$ 的，所以只需要一个 $d\times n$ 的变换矩阵 $\boldsymbol{W}_a$ 就可以将它变成 $n\times n$ 了，即

这其实就相当于把 $\boldsymbol{K}$ 固定为常数矩阵 $\boldsymbol{W}_a^{\top}$ 了。当然，原论文还做得更复杂一些，用到了两层 Dense 层：

但思想上并没有什么变化。

Random 形式

刚才说 Dense 形式相当于把 $\boldsymbol{K}$ 固定为常数矩阵，我们还能不能更“异想天开”一些：把 $\boldsymbol{Q}$ 固定为常数矩阵？这时候整个 $\boldsymbol{B}$ 相当于是一个常数矩阵，即

原论文中还真是实验了这种形式，称之为 Random，顾名思义，就是 $\boldsymbol{B}$ 是随机初始化的，然后可以选择随训练更新或不更新。据原论文描述，固定形式的 Attention 首次出现在论文《Fixed Encoder Self-Attention Patterns in Transformer-Based Machine Translation》，不同点是那里的 Attention 矩阵是由一个函数算出来的，而 Google 这篇论文则是完全随机初始化的。从形式上看，Random 实际上就相当于可分离卷积 (Depthwise Separable Convolution) 运算。

低秩分解

上面两种新形式，往往会面对着参数过多的问题，所以很自然地就想到通过低秩分解来降低参数量。对于 Dense 和 Random，原论文也提出并验证了对应的低秩分解形式，分别称为 Factorized Dense 和 Factorized Random。

Factorized Dense 通过 Dense 的方式，生成两个 $n\times a, n\times b$ 的矩阵 $\boldsymbol{B}_1,\boldsymbol{B}_2$，其中 $ab=n$；然后将 $\boldsymbol{B}_1$ 重复 $b$ 次、然后将 $\boldsymbol{B}_2$ 重复 $a$ 次，得到对应的 $n\times n$ 矩阵 $\tilde{\boldsymbol{B}}_1,\tilde{\boldsymbol{B}}_2$，最后将它们逐位相乘（个人感觉相乘之前 $\tilde{\boldsymbol{B}}_2$ 应该要转置一下比较合理，但原论文并没有提及），合成一个 $n\times n$ 的矩阵：

至于 Factorized Random 就很好理解了，本来是一整个 $n\times n$ 的矩阵 $\boldsymbol{R}$，现在变成两个 $n\times k$ 的矩阵 $\boldsymbol{R}_1,\boldsymbol{R}_2$，然后

混合模式

到目前为止，连同标准的自注意力，我们有 5 种不同的生成矩阵 $\boldsymbol{B}$ 的方案，它们也可以混合起来，即

其中 $\boldsymbol{B}i$ 是不同形式的自注意力矩阵，而 $\sum\limits{i=1}^N \alpha_i=1$ 是可学习参数。

结果分析

前面介绍了统称为 Synthesizer 的几种新型自注意力形式，它们的共同特点是没有保持“token 对 token”形式，尤其是 Random，则完全抛弃了原有注意力的动态特点，变成了静态的矩阵。

那么，这些新型自注意力的效果如何呢？

第一个评测任务是机器翻译，详细地比较了各种自注意力形式的效果：

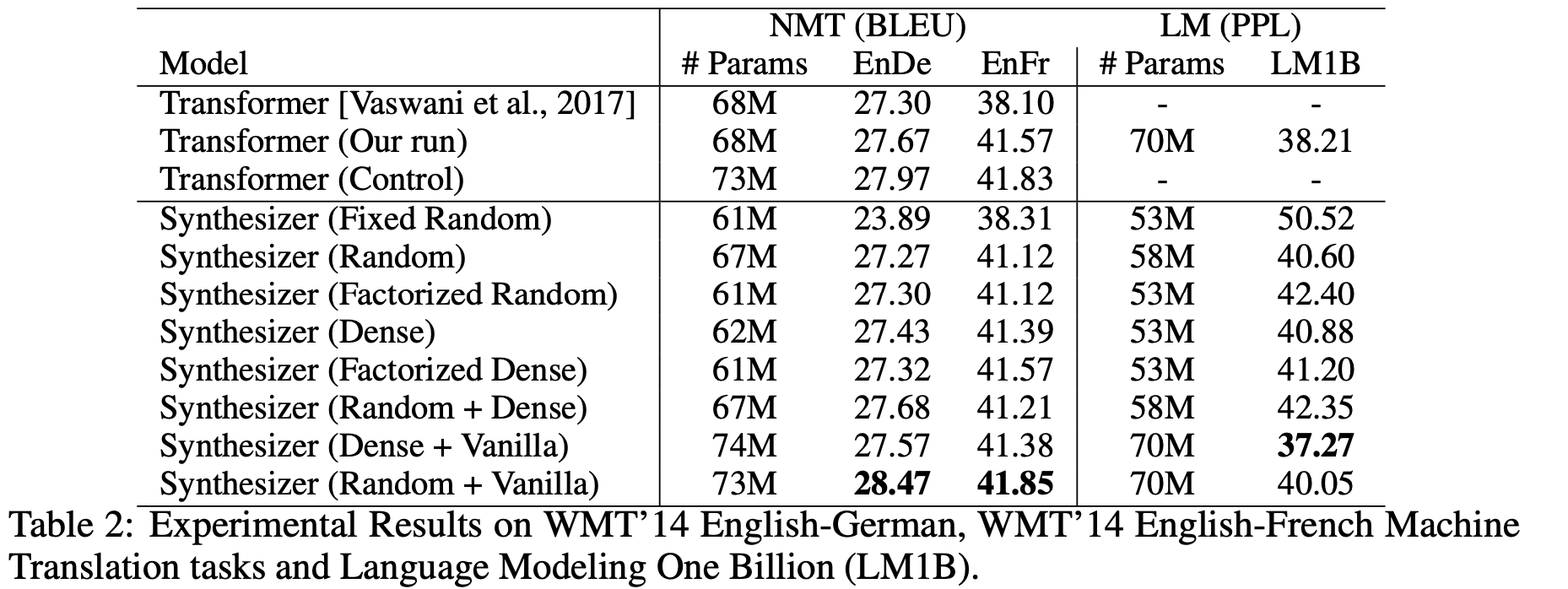
不知道读者怎么想，反正 Synthesizer 的这些结果是冲击了笔者对自注意力的认知的。表格显示，除了固定的 Random 外，所有的自注意力形式表现基本上都差不多，而且就算是固定的 Random 也有看得过去的效果，这表明我们以往对自注意力的认知和解释都太过片面了，并没有揭示自注意力生效的真正原因。

接下来在摘要和对话生成任务上的结果：

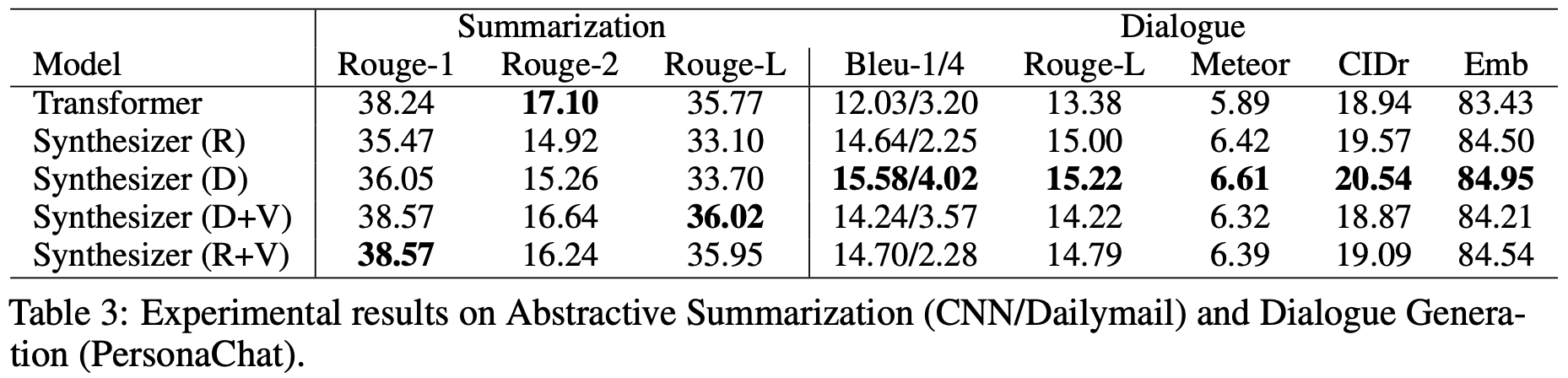
在自动摘要这个任务上，标准注意力效果比较好，但是对话生成这个任务上，结果则反过来：标准的自注意力是最差的，Dense (D) 和 Random (R) 是最好的，而当 Dense 和 Random 混合了标准的自注意力后 (即 D+V 和 R+V)，效果也变差了。这说明标准注意力并没有什么“独占鳌头”的优势，而几个 Synthesizer 看起来是标准注意力的“退化”，但事实上它们互不从属，各有优势。

最后，对于我们这些普通读者来说，可能比较关心是“预训练+微调”的效果怎样，也就是说，将 BERT 之类的模型的自注意力替换之后表现如何？原论文确实也做了这个实验，不过 Baseline 不是 BERT 而是 T5，结果如下：

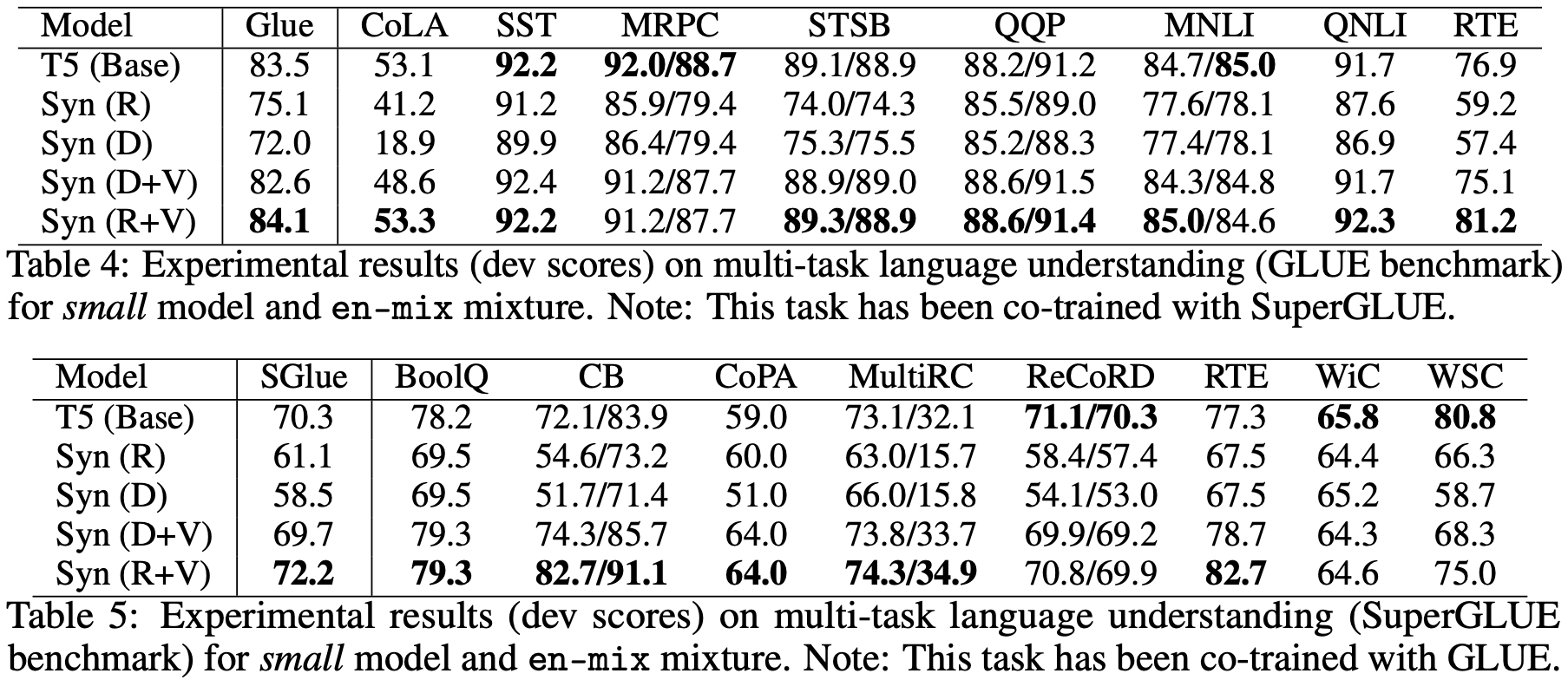
在这个结果中，相比标准自注意力，Dense 和 Random 就显得逊色了，这表明 Dense 和 Random 也许会在单一任务上表现得比较好，而迁移能力则比较弱。但是不能否定的是，像 Random 这样的自注意力，由于直接省去了 $\boldsymbol{Q}\boldsymbol{K}^{\top}$ 这个矩阵运算，因此计算效率会有明显提升，因此如果能想法子解决这个迁移性问题，说不准 Transformer 模型家族将会迎来大换血。

注意

原文直接转载自《Attention is All You Need》浅读（简介+代码），作者：苏建林。2019 年 8 月 27 日进行了更新，添加了同一作者的另一篇文章《为节约而生：从标准Attention到稀疏Attention》的内容。2020 年 6 月 14 日进行了更新，添加了同一作者的另一篇文章《Google新作Synthesizer：我们还不够了解自注意力》的内容。本文对三篇文章的内容进行了整合，部分地方有删改。