自从 2017 年 Google《Attention is All You Need》一文发布后,各种基于 Multi-Head Attention 的方法和模型层出不穷,文中提出的 Transformer 模型更是成为了自然语言处理 (NLP) 领域的标配。尤其是 2019 年在 NAACL 上正式发布的 BERT 模型,在一系列任务上都取得了优异的性能表现,将 Transformer 模型的热度推上了又一个高峰。
目前大部分的研究者都直接使用已有的 Python 包来进行实验(例如适用于 PyTorch 框架的 Transformers,以及适用于 Keras 框架的 bert4keras),这固然很方便,但是并不利于深入理解模型结构,尤其是对于 NLP 研究领域的入门者。
本文从介绍模型结构出发,使用 Keras 框架,手把手地带大家实现一个 Transformer block。
Attention 框架
NLP 以自然语言文本为研究对象,因此各种神经网络模型的本质,就是对词语序列进行编码。常规的做法,首先将每个词语都转化为对应的词向量,这样一个文本就变成了一个矩阵 $\boldsymbol{X} = (\boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_n)$,其中 $\boldsymbol{x}_i$ 就表示第 $i$ 个词的词向量,维度为 $d$,即 $\boldsymbol{X}\in \mathbb{R}^{n\times d}$。
在 Transformer 模型提出之前,对词语序列 $\boldsymbol{X}$ 的常规编码方式是通过循环网络 RNN 和卷积网络 CNN。
-
RNN 模型(例如 LSTM、GRU)的方案很简单,每一个词语 $\boldsymbol{x}_t$ 对应的编码结果 $\boldsymbol{y}_t$ 通过递归地计算得到:
\[\boldsymbol{y}_t =f(\boldsymbol{y}_{t-1},\boldsymbol{x}_t) \tag{1}\]但是 RNN 结构的明显缺点之一就是无法并行,因此计算速度较慢;
-
CNN 模型的方案也很简单,通过滑动窗口来编码词语序列,例如尺寸为 3 的卷积,即每个词使用自身以及前一个和后一个词来编码:
\[\boldsymbol{y}_t = f(\boldsymbol{x}_{t-1},\boldsymbol{x}_t,\boldsymbol{x}_{t+1}) \tag{2}\]CNN 能够并行地计算,因此速度很快。但是因为 CNN 通过窗口来进行编码,因此更侧重于捕获局部信息,难以建模长距离的语义依赖。
Google 通过《Attention is All You Need》提供了第三个方案:直接使用注意力 Attention 机制进行编码。相比 RNN 要逐步递归才能获得全局信息(因此一般使用双向 RNN),而 CNN 事实上只能获取局部信息,需要通过层叠来增大感受野,Attention 机制一步到位获取了全局信息:
\[\boldsymbol{y}_t = f(\boldsymbol{x}_t,\boldsymbol{A},\boldsymbol{B}) \tag{3}\]其中 $\boldsymbol{A},\boldsymbol{B}$ 是另外的词语序列(矩阵),如果取 $\boldsymbol{A}=\boldsymbol{B}=\boldsymbol{X}$,那么就称为 Self Attention,即直接将 $\boldsymbol{x}_t$ 与自身序列中的每个词进行比较,最后算出 $\boldsymbol{y}_t$。
Attention
前面我们介绍的是 Attention 一般化的框架描述,Google 在论文中则给出了具体的模型方案:
\[\text{Attention}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = \text{softmax}\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{V} \tag{4}\]其中 $\boldsymbol{Q}\in\mathbb{R}^{n\times d_k}, \boldsymbol{K}\in\mathbb{R}^{m\times d_k}, \boldsymbol{V}\in\mathbb{R}^{m\times d_v}$。如果忽略 softmax 激活函数,实际上它就是三个 $n\times d_k,d_k\times m, m\times d_v$ 矩阵相乘,得到一个 $n\times d_v$ 的矩阵。即 Attention 将 $n\times d_k$ 的序列 $\boldsymbol{Q}$ 编码成了一个新的 $n\times d_v$ 的序列。
Attention 的公式拆开逐个向量来看更加清楚:
\[\text{Attention}(\boldsymbol{q}_t,\boldsymbol{K},\boldsymbol{V}) = \sum_{s=1}^m \frac{1}{Z}\exp\left(\frac{\langle\boldsymbol{q}_t, \boldsymbol{k}_s\rangle}{\sqrt{d_k}}\right)\boldsymbol{v}_s \tag{5}\]其中 $Z$ 是归一化因子。$\boldsymbol{K},\boldsymbol{V}$ 是一一对应的 key-value 的关系,Attention 就是通过 $\boldsymbol{q}_t$ 这个 query 与各个 $\boldsymbol{k}_s$ 内积的并 softmax 的方式,来得到 $\boldsymbol{q}_t$ 与各个 $\boldsymbol{v}_s$ 的相似度,然后加权求和,得到一个 $d_v$ 维的向量。其中因子 $\sqrt{d_k}$ 起到调节作用,使得内积不至于太大。
Multi-Head Attention
Multi-Head Attention 可以看作是 Attention 机制的完善,它首先 $\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$ 通过参数矩阵映射,然后再做 Attention,并且把这个过程重复做 $h$ 次,最后将结果拼接起来,这使得模型能够捕获到更加复杂的特征信息:
\[\begin{gather}head_i = \text{Attention}(\boldsymbol{Q}\boldsymbol{W}_i^Q,\boldsymbol{K}\boldsymbol{W}_i^K,\boldsymbol{V}\boldsymbol{W}_i^V)\\ \text{MultiHead}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = \text{Concat}(head_1,...,head_h) \end{gather} \tag{6}\]其中 $\boldsymbol{W}_i^Q\in\mathbb{R}^{d_k\times \tilde{d}_k}, \boldsymbol{W}_i^K\in\mathbb{R}^{d_k\times \tilde{d}_k}, \boldsymbol{W}_i^V\in\mathbb{R}^{d_v\times \tilde{d}_v}$ 是映射矩阵。最后多头的结果拼接起来,得到最终 $n\times (h\tilde{d}_v)$ 的编码结果序列。所谓“多头” (Multi-Head),其实只是多做几次 Attention(参数不共享),然后把结果拼接。
如果取 $\boldsymbol{Q}=\boldsymbol{K}=\boldsymbol{V}=\boldsymbol{X}$,即 $\text{Attention}(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})$,就被称为 Self Attention,也就是在序列内部做Attention,寻找序列内部词语之间的联系。更准确来说,Google 所用的是 Self Multi-Head Attention:
\[\boldsymbol{Y}=MultiHead(\boldsymbol{X},\boldsymbol{X},\boldsymbol{X})\tag{7}\]
因此,Multi-Head Attention 的结构实际上并不复杂,用 Keras 实现也很容易,正所谓“大道至简”:
from keras.layers import *
import keras.backend as K
import tensorflow as tf
class MultiHeadAttention(Layer):
"""
# Input
three 3D tensor: Q, K, V
each with shape: `(samples, steps, features)`.
# Output shape
3D tensor with shape: `(samples, input0 steps, head number * head size)`.
Note: The layer has been tested with Keras 2.3.1 (Tensorflow 1.14.0 as backend)
Example:
S_inputs = Input(shape=(None,), dtype='int32')
embeddings = Embedding(max_features, 128)(S_inputs)
result_seq = MultiHeadAttention(8,16)([embeddings,embeddings,embeddings]) # self Attention
result_vec = GlobalMaxPool1D()(result_seq)
result_vec = Dropout(0.5)(result_vec)
outputs = Dense(1, activation='sigmoid')(result_vec)
"""
def __init__(self, heads, size_per_head, key_size=None, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.heads = heads
self.size_per_head = size_per_head
self.out_dim = heads * size_per_head
self.key_size = key_size if key_size else size_per_head
def get_config(self):
config = super().get_config()
config['heads'] = self.heads
config['size_per_head'] = self.size_per_head
config['key_size'] = self.key_size
return config
def build(self, input_shape):
super(MultiHeadAttention, self).build(input_shape)
self.q_dense = Dense(units=self.key_size * self.heads, use_bias=False)
self.k_dense = Dense(units=self.key_size * self.heads, use_bias=False)
self.v_dense = Dense(units=self.out_dim, use_bias=False)
def call(self, inputs):
Q_seq, K_seq, V_seq = inputs
Q_seq = self.q_dense(Q_seq)
K_seq = self.k_dense(K_seq)
V_seq = self.v_dense(V_seq)
Q_seq = K.reshape(Q_seq, (-1, K.shape(Q_seq)[1], self.heads, self.key_size))
K_seq = K.reshape(K_seq, (-1, K.shape(K_seq)[1], self.heads, self.key_size))
V_seq = K.reshape(V_seq, (-1, K.shape(V_seq)[1], self.heads, self.size_per_head))
Q_seq = K.permute_dimensions(Q_seq, (0, 2, 1, 3))
K_seq = K.permute_dimensions(K_seq, (0, 2, 1, 3))
V_seq = K.permute_dimensions(V_seq, (0, 2, 1, 3))
# Attention
A = tf.einsum('bjhd,bkhd->bhjk', Q_seq, K_seq) / self.key_size**0.5
A = K.softmax(A)
O_seq = tf.einsum('bhjk,bkhd->bjhd', A, V_seq)
O_seq = K.permute_dimensions(O_seq, (0, 2, 1, 3))
O_seq = K.reshape(O_seq, (-1, K.shape(O_seq)[1], self.out_dim))
return O_seq
def compute_output_shape(self, input_shape):
return (input_shape[0][0], input_shape[0][1], self.out_dim)
我们以 IMDB 电影评论情感极性任务为例,使用 Multi-Head Attention 模型对文本进行二分类:
from keras.preprocessing import sequence
from keras.datasets import imdb
from keras.models import Model
max_features = 20000
maxlen = 80
batch_size = 32
print('Loading data...')
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=max_features)
print(len(x_train), 'train sequences')
print(len(x_test), 'test sequences')
print('Pad sequences (samples x time)')
x_train = sequence.pad_sequences(x_train, maxlen=maxlen)
x_test = sequence.pad_sequences(x_test, maxlen=maxlen)
print('x_train shape:', x_train.shape)
print('x_test shape:', x_test.shape)
S_inputs = Input(shape=(None,), dtype='int32')
embeddings = Embedding(max_features, 128)(S_inputs)
O_seq = MultiHeadAttention(8,16)([embeddings,embeddings,embeddings])
O_seq = GlobalAveragePooling1D()(O_seq)
O_seq = Dropout(0.5)(O_seq)
outputs = Dense(1, activation='sigmoid')(O_seq)
model = Model(inputs=S_inputs, outputs=outputs)
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
print('Train...')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=5,
validation_data=(x_test, y_test))
Train on 25000 samples, validate on 25000 samples
Epoch 1/5
25000/25000 [==============================] - 63s 3ms/step - loss: 0.4145 - accuracy: 0.8060 - val_loss: 0.3498 - val_accuracy: 0.8456
Epoch 2/5
25000/25000 [==============================] - 54s 2ms/step - loss: 0.2529 - accuracy: 0.8991 - val_loss: 0.4009 - val_accuracy: 0.8254
Epoch 3/5
25000/25000 [==============================] - 51s 2ms/step - loss: 0.1773 - accuracy: 0.9316 - val_loss: 0.4754 - val_accuracy: 0.8199
Epoch 4/5
25000/25000 [==============================] - 48s 2ms/step - loss: 0.1210 - accuracy: 0.9563 - val_loss: 0.6369 - val_accuracy: 0.8010
Epoch 5/5
25000/25000 [==============================] - 50s 2ms/step - loss: 0.0798 - accuracy: 0.9722 - val_loss: 0.8074 - val_accuracy: 0.8001
Transformer
标准的 Transformer 模型由 Encoder 和 Decoder 两个部分组成,如下图所示:
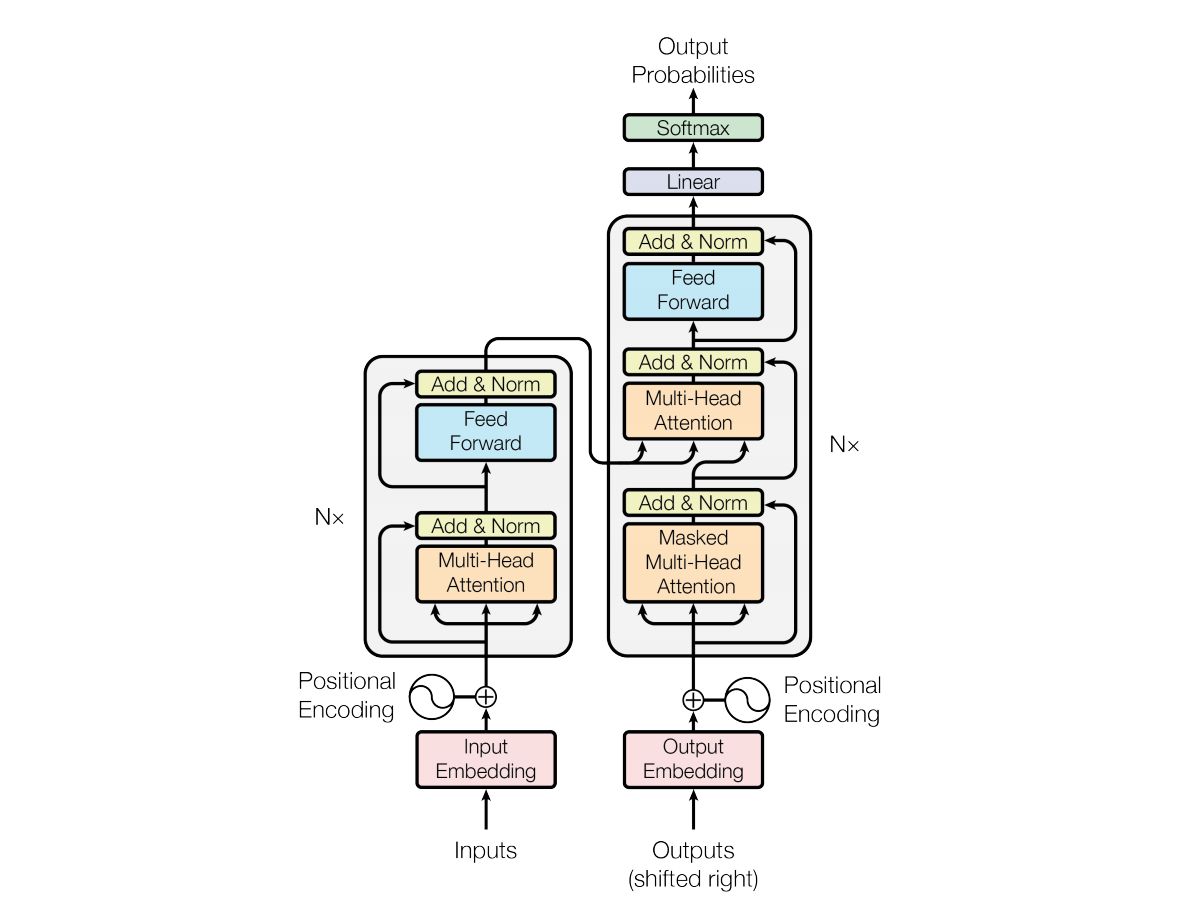
本文主要关注于 Encoder 部分,这也是一种常用的基于 Multi-Head Attention 的编码器,称为 Transformer block,通常会堆叠 $N$ 个使用,如上图所示。Transformer block 除了 Multi-Head Attention 模块以外,还会包含一个前向全连接网络层 (fully connected feed-forward network)、两个残差连接 (residual connection) & 正则化层 (normalisation):
from keras.models import Sequential
class LayerNormalization(Layer):
def __init__(
self,
center=True,
scale=True,
epsilon=None,
**kwargs
):
super(LayerNormalization, self).__init__(**kwargs)
self.center = center
self.scale = scale
self.epsilon = epsilon or 1e-12
def get_config(self):
config = super(LayerNormalization, self).get_config()
config['center'] = self.center
config['scale'] = self.scale
config['epsilon'] = self.epsilon
return config
def build(self, input_shape):
super(LayerNormalization, self).build(input_shape)
shape = (input_shape[-1],)
if self.center:
self.beta = self.add_weight(
shape=shape, initializer='zeros', name='beta'
)
if self.scale:
self.gamma = self.add_weight(
shape=shape, initializer='ones', name='gamma'
)
def call(self, inputs):
if self.center:
beta = self.beta
if self.scale:
gamma = self.gamma
outputs = inputs
if self.center:
mean = K.mean(outputs, axis=-1, keepdims=True)
outputs = outputs - mean
if self.scale:
variance = K.mean(K.square(outputs), axis=-1, keepdims=True)
std = K.sqrt(variance + self.epsilon)
outputs = outputs / std * gamma
if self.center:
outputs = outputs + beta
return outputs
def compute_output_shape(self, input_shape):
return input_shape
class TransformerBlock(Layer):
"""
# Input
3D tensor: `(samples, steps, features)`.
# Output shape
3D tensor with shape: `(samples, input steps, head number * head size)`.
Note: The layer has been tested with Keras 2.3.1 (Tensorflow 1.14.0 as backend)
Example:
S_inputs = Input(shape=(None,), dtype='int32')
embeddings = Embedding(max_features, 128)(S_inputs)
result_seq = TransformerBlock(8,16,128)(embeddings)
result_vec = GlobalMaxPool1D()(result_seq)
result_vec = Dropout(0.5)(result_vec)
outputs = Dense(1, activation='sigmoid')(result_vec)
"""
def __init__(self, heads, size_per_head, ff_dim, rate=0.1, **kwargs):
super(TransformerBlock, self).__init__(**kwargs)
self.heads = heads
self.size_per_head = size_per_head
self.ff_dim = ff_dim
self.rate = rate
def get_config(self):
config = super().get_config()
config['heads'] = self.heads
config['size_per_head'] = self.size_per_head
config['ff_dim'] = self.ff_dim
config['rate'] = self.rate
return config
def build(self, input_shape):
super(TransformerBlock, self).build(input_shape)
assert input_shape[-1] == self.heads * self.size_per_head
self.att = MultiHeadAttention(heads=self.heads, size_per_head=self.size_per_head)
self.ffn = Sequential([
Dense(self.ff_dim, activation="relu"),
Dense(self.heads * self.size_per_head),
])
self.layernorm1 = LayerNormalization(epsilon=1e-6)
self.layernorm2 = LayerNormalization(epsilon=1e-6)
self.dropout1 = Dropout(self.rate)
self.dropout2 = Dropout(self.rate)
def call(self, inputs):
attn_output = self.att([inputs, inputs, inputs])
attn_output = self.dropout1(attn_output)
out1 = self.layernorm1(inputs + attn_output)
ffn_output = self.ffn(out1)
ffn_output = self.dropout2(ffn_output)
return self.layernorm2(out1 + ffn_output)
同样地,我们以 IMDB 电影评论情感极性任务为例,使用 TransformerBlock 模型对文本进行二分类:
max_features = 20000
maxlen = 80
batch_size = 32
print('Loading data...')
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=max_features)
print(len(x_train), 'train sequences')
print(len(x_test), 'test sequences')
print('Pad sequences (samples x time)')
x_train = sequence.pad_sequences(x_train, maxlen=maxlen)
x_test = sequence.pad_sequences(x_test, maxlen=maxlen)
print('x_train shape:', x_train.shape)
print('x_test shape:', x_test.shape)
S_inputs = Input(shape=(None,), dtype='int32')
embeddings = Embedding(max_features, 128)(S_inputs)
O_seq = TransformerBlock(8,16, 128)(embeddings)
O_seq = GlobalAveragePooling1D()(O_seq)
O_seq = Dropout(0.5)(O_seq)
outputs = Dense(1, activation='sigmoid')(O_seq)
model = Model(inputs=S_inputs, outputs=outputs)
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
print('Train...')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=5,
validation_data=(x_test, y_test))
Train on 25000 samples, validate on 25000 samples
Epoch 1/5
25000/25000 [==============================] - 73s 3ms/step - loss: 0.4618 - accuracy: 0.7796 - val_loss: 0.4023 - val_accuracy: 0.8205
Epoch 2/5
25000/25000 [==============================] - 72s 3ms/step - loss: 0.3023 - accuracy: 0.8761 - val_loss: 0.4148 - val_accuracy: 0.8150
Epoch 3/5
25000/25000 [==============================] - 71s 3ms/step - loss: 0.2356 - accuracy: 0.9057 - val_loss: 0.4447 - val_accuracy: 0.8138
Epoch 4/5
25000/25000 [==============================] - 71s 3ms/step - loss: 0.1943 - accuracy: 0.9250 - val_loss: 0.4779 - val_accuracy: 0.8121
Epoch 5/5
25000/25000 [==============================] - 71s 3ms/step - loss: 0.1616 - accuracy: 0.9398 - val_loss: 0.5316 - val_accuracy: 0.8062
参考
[1] 《Attention is All You Need》浅读(简介+代码)
[2] https://github.com/bojone/attention
[3] Text classification with Transformer