同指消解 (Coreference Resolution),又称指代消解,是自然语言处理中的一个基础任务,即判断两个描述 (mention) 是否指向现实世界中的同一个对象。根据描述类型的不同,可以分为:
-
实体同指消解
实体就是我们常说的人物、组织机构、时间、地点等元素,在自然语言处理中通过专门的命名实体识别 (Named Entity Recognition, NER) 任务进行研究,更宽泛意义上的实体定义还包括代词,例如他、该公司、这些机构等。
实体同指消解任务就负责将指向现实世界中同一实体的所有实体描述连接起来,形成同指簇(或同指链),在同一个簇中(链上)的所有实体描述都互相同指。
-
事件同指消解
事件是指由某些参与者在某个时间某个地点发生的行为,其中能够明显表明事件发生的词被称为触发词 (Trigger),一般就是动词,例如“杀”就明显标记了一个攻击事件的发生,或者说“杀”触发了一个攻击事件。事件的参与人物、组织,发生的时间、地点等称为事件的论元 (Argument)。
对于事件参与者,我们通常只关心实施者(称为施事者)和接受者(称为受事者),分别用 $Arg0$ 和 $Arg1$ 来表示,例如“张三杀了李四”,那么张三就是施事者(攻击事件中的攻击者),李四就是受事者(攻击事件中的受害者)。因此,事件可以用一个五元组来表示:
\[\text{Event} = (\text{Trigger, Arg0, Arg1, Time, Location})\]我们通常将包含触发词和论元的文本片段称为对应事件的事件描述,更狭隘定义下的事件描述只包含触发词。
与实体类似,事件同指消解就负责将指向现实世界中同一事件的所有事件描述连接起来,形成同指簇(或同指链),在同一个簇中(链上)的所有事件描述都互相同指。
可以看到,相比实体同指只需要匹配两个词语(短语),事件同指的判断更加复杂,需要匹配两个事件描述中对应的触发词和所有的论元。由于事件描述多种多样,只在很少情况下事件描述中会包含完整的论元信息(即上面的五元组),通常描述中只会出现其中某几个论元甚至只有触发词,因此需要从上下文中挖掘线索。更麻烦的是,大量的论元是以代词的形式存在,如果想要获取到这些论元的有效信息,还需要进行实体同指消解。
因此,实体同指消解和事件同指消解虽然任务定义非常相似,但是由于实体和事件本身结构的不同(实体只是词语或短语,而事件是触发词-论元结构),事件同指的难度要大大超过实体同指。而且,由于事件论元本身也是实体,因此要获取有效的实体信息,有时还需要依赖于实体同指的结果。
同指消解框架
三个核心问题
同指消解任务可以简化为是一个描述对 (mantion-pair) 分类问题,每次输入两个描述(实体描述或事件描述),通过匹配模型判断它们是否同指。
同指消解任务本质上是一个聚类问题,对描述对分类相当于是在度量它们之间的距离,因此也可以直接采用聚类框架来完成,即对于每一个描述,要么加入已有的同指簇,要么另起新的簇。后面我们会详细介绍。
因此,我们需要解决的核心问题有三个:
- 怎样从生文本中识别实体/事件描述(包括怎样缓解错误传递);
- 怎样建模识别出的实体/事件描述;
- 怎样匹配描述对。
对于第一个问题,目前主流的方法是将其看作是一个文本片段 (span) 分类任务,即首先将文本拆分成可以重叠的文本片段,然后判断每一个文本片段是否是实体或触发词。当然,也可以将其看作是序列标注任务,采用 BIO 或者 IO 标签的形式,预测序列中实体或触发词对应的词语 (token) 位置。由于进行同指消解前需要先识别出描述,因此不可避免地会存在错误传递的问题。对于管道模型这个问题尤其严重,也有工作尝试通过门控机制来过滤噪声 (Lai & Ji, 2021),而联合 (joint) 模型 (Lee et al., 2017) 由于是联合地完成描述识别和同指消解,因此能够更自然地缓解级联错误。
对于第二个问题,目前大部分工作专注于对实体或事件触发词进行编码,即首先将整个文档送入编码器学习语义表示,将文本转换为词语向量序列(BERT 等有长度限制,需要对文档进行切片),然后取出实体或触发词对应的向量(多个词则进行池化操作)作为实体或事件的语义表示。
当然了,对于事件而言,虽然触发词是核心,但是论元也很重要,因此也有部分工作通过语义角色标注 SRL (Choubey & Huang, 2017; Barhom et al., 2019)、抽象语义表示 AMR 图 (Wang et al., 2021) 等方法识别论元,然后将论元信息也添加到事件表示中去。但是,识别论元、判断论元角色、将论元和对应的触发词相关联也会引入额外的错误。近年来,随着图模型的发展,以及对事件图谱的探索 (Guan et al., 2021),以“实体-事件”为核心的各种图结构表示也被用于编码事件表示 (Tran et al., 2021)。
对于第三个问题,最直接的做法就是拼接建模好的实体/事件表示,以及一些人工构建的特征,然后直接通过前馈神经网络 FFNN 进行分类。考虑到我们对每一个描述对 (mention-pair) 的判断只是局部的同指判断结果,可能在全局层面存在矛盾,并且随着同指消解的进行,已有的同指判断结果(已构建出的同指簇)也能为后续的同指判断提供辅助,因此诸如精炼描述 (Span Refinement) 等操作也被很多工作 (Lee et al., 2018; Fei et al., 2019; Joshi et al., 2019, 2020) 采用以进行高层推理 (Higher-Order Inference, HOI)。
端到端通用框架
2017 年 Lee 等人提出了第一个端到端的实体同指消解框架,后续的很多工作都沿用了该框架,甚至将其迁移用于事件同指消解。
具体地,假设文档 $D$ 中共包含 $T$ 个词语,首先可以创建出 $N=\frac{T(T+1)}{2}$ 个可能的文本片段,然后按照片段的起始和结束索引对所有片段进行排序。同指消解就是判断每个片段与它前面的哪些片段同指,也就是对每一个片段 $i$,从 $\mathcal{Y}(i) = {\epsilon,1,…,i-1}$ 中为其分配前情 (antecedent) $y_i$,前情为 $j$ 就意味着片段 $i$ 和片段 $j$ 同指 ($1\le j\le i-1$),前情为空 $\epsilon$ 则表示片段 $i$ 不是描述,或者它是描述,但是不与任何前面的片段同指。
同指消解框架就是学习一个最可能生成正确同指簇的条件概率分布 $P(y_1,…,y_N\mid D)$:
\[\begin{align} P(y_1,...,y_N\mid D) &= \prod_{i=1}^N P(y_i\mid D)\\ &=\prod_{i=1}^N \frac{\exp(s(i, y_i))}{\sum_{y' \in \mathcal{Y}(i)} \exp(s(i,y'))} \end{align} \tag{1}\]其中 $s(i,j)$ 就是片段 $i$ 和片段 $j$ 的 pairwise 同指分数,它包含三个部分:1) 片段 $i$ 是否为描述,2) 片段 $j$ 是否为描述,3) 片段 $j$ 是否是 $i$ 的前情:
\[s(i,j) = \begin{cases} 0 & j=\epsilon \\ s_m(i) + s_m(j) + s_a(i,j) & j \neq \epsilon \end{cases} \tag{2}\]其中,$s_m(i)$ 是片段 $i$ 为描述的得分,$s_a(i,j)$ 是片段 $j$ 为片段 $i$ 的前情的 pairwise 得分,它们可以直接通过前馈神经网络 FFNN 得到,$\phi(i,j)$ 表示人工构建的特征向量:
\[\begin{align} s_m(i) &= \boldsymbol{w}_m \cdot \text{FFNN}_m(\boldsymbol{g}_i)\\ s_a(i,j) &=\boldsymbol{w}_a \cdot \text{FFNN}_a([\boldsymbol{g}_i, \boldsymbol{g}_j,\boldsymbol{g}_i \circ \boldsymbol{g}_j,\phi(i,j)]) \end{align} \tag{3}\]但是这个框架的空间复杂度非常高:记录所有片段的语义表示需要 $\mathcal{O}(T^2)$ 的空间复杂度,而保存所有的片段对 (span pair) 的空间复杂度更是达到 $\mathcal{O}(T^4)$。因此在训练和预测时都需要对候选片段进行裁剪,例如:
- 在创建文本片段时,限定最大长度只能包含 $L$ 个词语;
- 计算所有文本片段的描述得分 $s_m(i)$,只保留描述得分最高的前 $\lambda T$ 个片段;
- 通过一些轻量计算得分(比如 $s_c(i,j) = \boldsymbol{g}_i^\top \textbf{W}_c \boldsymbol{g}_j$)对片段对 (span pair) 进行剪裁,对于每个片段只保留得分最高的前 $K$ 个候选前情。
由于每个片段 $i$ 的前情信息是通过 gold 同指簇来提供的,并且每个片段可能有多个前情,因此学习目标式 $(1)$ 可以细化为:
\[\log \prod_{i=1}^N \sum_{\hat{y}\in\mathcal{Y}(i) \cap \text{GOLD}(i)} P(\hat{y}) \tag{4}\]其中,$\text{GOLD}(i)$ 是片段 $i$ 所在的 gold 同指簇,如果片段 $i$ 不属于任何一个 gold 同指簇或者它所有的 gold 前情都被剪裁掉了,那么 $\text{GOLD}(i) = {\epsilon}$。
通过优化 $(4)$ 式模型自然地就能学会修剪片段,虽然最初的修剪是完全随机的,但只有 gold 描述会收到正向的更新,模型可以利用此学习信号对 $s(i,j)$ 中的不同部分进行信用分配。并且式 $(3)$ 中将虚拟前情的分数固定为 0,可以防止描述抽取和裁剪引入噪声。
实体同指消解
端到端通用框架除了空间复杂度高之外,还有一个问题就是做出的描述对同指判断可能在全局层面存在矛盾,例如根据局部的信息判断出 $A$ 和 $B$ 同指,$B$ 和 $C$ 同指,但是实际上 $A$ 和 $C$ 是不同指的。因此,之后的许多工作都专注于利用已经预测出的同指簇信息来辅助后续的同指判断,进行高层推理 (Higher-Order Inference)。
除了端到端通用框架以外,还有一些工作使用了不同的框架来进行实体同指,例如 Wu 等人 (2020) 将同指任务转换为 QA 任务来解决、Xia 等人 (2020) 采用一种增量聚类算法来完成同指。
片段精炼
片段精炼 (Span Refinement) 是最广为采用的高层推理方法,它由 Lee 等人在 2018 年首次提出,后续的工作 (Fei et al., 2019; Joshi et al., 2019, 2020) 都采用了类似的方法。片段精炼的想法非常简单,每一个片段都通过对应的前情分布来获得增强表示,从而隐式地引入已预测出的同指簇信息。
具体地,每一个片段 $i$ 都通过 $N$ 轮迭代来精炼片段表示,记第 $n$ 轮的表示为 $\boldsymbol{g}_i^n$,它通过运用注意力机制对前一轮表示 $\boldsymbol{g}_j^{n-1}$ 的加权求和得到,注意力机制的权重取决于片段 $j$ 为片段 $i$ 前情的概率(可以将编码器的输出语义表示作为片段的初始表示 $\boldsymbol{g}_i^1$)。而且精炼表示反过来也能帮助模型获得更好的前情分布 $P_n(y_i)$:
\[P_n(y_i) = \frac{e^{s(\boldsymbol{g}_i^n,\boldsymbol{g}_{y_i}^n)}}{\sum_{y\in \mathcal{Y}(i)}e^{s(\boldsymbol{g}_i^n,\boldsymbol{g}_y^n)}} \tag{5}\]每轮迭代时,我们首先以片段 $i$ 的前情分布 $P_n(y_i)$ 作为注意力权重来生成其对应的前情表示 $\boldsymbol{a}_i^n$:
\[\boldsymbol{a}_i^n = \sum_{y_i \in \mathcal{Y}(i)} P_n(y_i)\cdot \boldsymbol{g}_{y_i}^n \tag{6}\]然后通过门控机制将前情表示 $\boldsymbol{a}_i^n$ 融入到当前片段表示 $\boldsymbol{g}_i^n$,从而得到新的片段表示 $\boldsymbol{g}_i^{n+1}$:
\[\begin{align} \boldsymbol{f}_i^n &= \sigma(\textbf{W}_f [\boldsymbol{g}_i^n,\boldsymbol{a}_i^n])\\ \boldsymbol{g}_i^{n+1} &= \boldsymbol{f}_i^n \circ\boldsymbol{g}_i^n + (1-\boldsymbol{f}_i^n)\circ\boldsymbol{a}_i^n \end{align} \tag{7}\]这种通过 Span-ranking 结构来获取前情分布的方法也可以看作是预测隐藏的前情树 (Fernandes et al., 2012; Martschat & Strube, 2015),每个片段 $i$ 预测出的前情就是它的父节点,每棵树就是一个预测出的簇。迭代地精炼片段表示和前情分布也可以理解为是在隐式地建模前情树中的有向路径。
当然,片段精炼方法也有一些变体,例如 Entity Equalization (Kantor & Globerson, 2019) 和 Span Clustering (Xu & Choi, 2020),不过它们的想法都是利用片段的前情信息(已预测出的簇)来增强片段表示。
虽然片段精炼方法被许多工作采用,认为能够通过引入全局的信息改进端到端通用框架,但是根据 Xu & Choi (2020) 进行的分析显示,近年来模型性能的提升主要是来自于应用更强的编码器生成了更好的描述表示。与最近的 SpanBERT 编码器相比,目前所有的高层推理方法都无法进一步提升性能。
因此,生成更好的描述表示(表示学习)可能比语义匹配更重要。
减少空间复杂度
正如我们前面所说,端到端通用框架最大的缺点是空间复杂度高,如果不进行裁剪,模型需要动态地计算所有可能的片段和片段对 (span-pair) 的表示,空间复杂度达到 $\mathcal{O}(T^4)$。因此,Kirstain 等人 (2021) 提出了一种减少空间复杂度的方法,其核心想法是将式 $(2)$ 中的描述得分 $s_m(\cdot)$ 和 pairwise 前情得分 $s_a(\cdot,\cdot)$ 的计算方式从基于片段转变为基于词语。
具体地,对于文本中每一个词语 (token) 编码后的表示 $\boldsymbol{x}$,首先分别计算其对应的描述 start 和 end 表示 $\boldsymbol{m^s}$ 和 $\boldsymbol{m}^e$:
\[\boldsymbol{m}^s = \text{GeLU}(\boldsymbol{W}_m^s\boldsymbol{x}) \quad\quad \boldsymbol{m}^e = \text{GeLU}(\boldsymbol{W}_m^e\boldsymbol{x})\]然后使用描述 start 和 end 表示来计算每一个片段 $i$ 的描述得分 $s_m(\cdot)$:
\[s_m(q) = \boldsymbol{v}_s\cdot\boldsymbol{m}_{i_s}^s + \boldsymbol{v}_e \cdot \boldsymbol{m}_{i_e}^e + \boldsymbol{m}_{i_s}^s\cdot\boldsymbol{B}_m\cdot\boldsymbol{m}_{i_e}^e \tag{8}\]其中,$i_s$ 和 $i_e$ 分别是片段 $i$ 的起始和结束词语,向量 $\boldsymbol{v}_s,\boldsymbol{v}_e$ 和矩阵 $\boldsymbol{B}_m$ 是模型的参数。前两项分别度量 $i_s$ 和 $i_e$ 为实体描述开始和结束的可能性,第三项则度量它们是否指向同一个实体的边界。虽然依然需要进行剪裁(片段最大长度为 $L$,只保留描述得分最高的前 $\lambda T$ 个片段),但是由于所有词语的描述 start 和 end 表示 $\boldsymbol{m^s}$ 和 $\boldsymbol{m}^e$ 都会被重复使用,因此大大降低了空间复杂度。
类似地,pairwise 前情得分 $s_a(\cdot,\cdot)$ 同样通过计算词语的前情 start 和 end 表示来得到:
\[\boldsymbol{a}^s = \text{GeLU}(\boldsymbol{W}_a^s\boldsymbol{x}) \quad\quad \boldsymbol{a}^e = \text{GeLU}(\boldsymbol{W}_a^e\boldsymbol{x})\] \[\begin{align} s_a(i,j) &= \boldsymbol{a}_{i_s}^s\cdot \boldsymbol{B}_a^{ss}\cdot \boldsymbol{a}_{j_s}^s + \boldsymbol{a}_{i_s}^s\cdot \boldsymbol{B}_a^{se}\cdot \boldsymbol{a}_{j_e}^e\\ &+ \boldsymbol{a}_{i_e}^e\cdot \boldsymbol{B}_a^{es}\cdot \boldsymbol{a}_{j_s}^s + \boldsymbol{a}_{i_e}^e\cdot \boldsymbol{B}_a^{ee}\cdot \boldsymbol{a}_{j_e}^e \end{align} \tag{9}\]也就是通过计算两个片段 $i$ 和 $j$ 的边界词语(片段 $i$ 的起始结束词语 $i_s,i_e$ 和片段 $j$ 的起始结束词语 $j_s,j_e$)的交互来度量它们同指的可能性,如下图所示。

式 $(9)$ 的计算实际上与先拼接边界词语表示再计算双线性变换是等价的:
\[s_a(i,j) = [\boldsymbol{a}_{i_s}^s;\boldsymbol{a}_{i_e}^e]\cdot\boldsymbol{B}_a\cdot[\boldsymbol{a}_{j_s}^s;\boldsymbol{a}_{j_e}^e] \tag{10}\]但是同样地,由于只需要存储词语的前情 start 和 end 表示,并且它们可以被重复使用,因此空间复杂度更低。
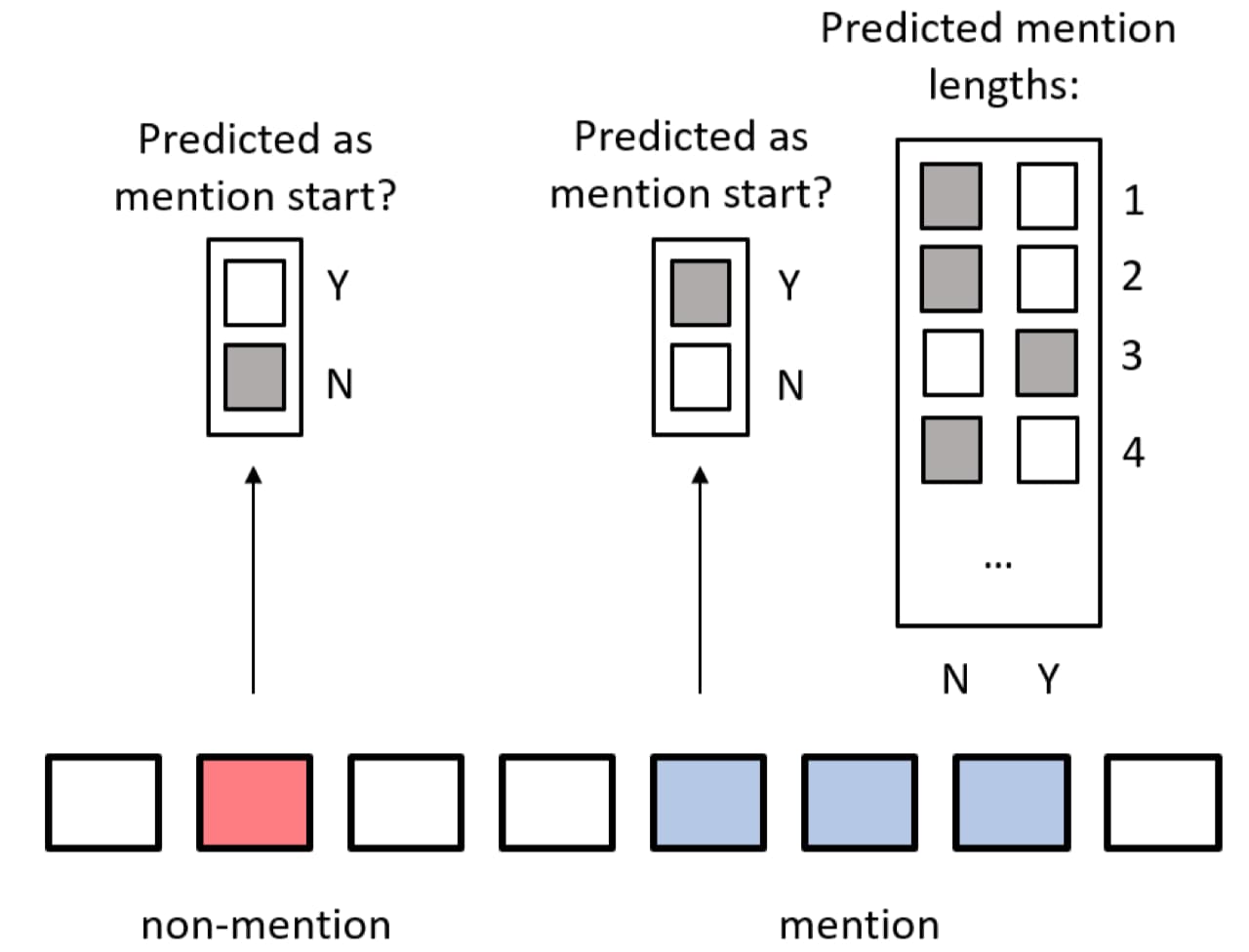
除此以外,对于描述抽取任务,Kriman 和 Ji (2021) 还提出了一种空间复杂度很低并且也能预测存在部分重叠的描述的方法,将描述抽取切分为两个子任务,分别用两个分类器来完成:
- 当前词语 (token) 是否是至少一个相关描述的起始;
- 从当前词语起始的所有描述的长度有哪些。
第一个是二分类问题,第二个是多标签分类任务(相同起始位置可以对应多个长度不同的描述),如下图所示:
增量聚类算法
同样为了降低模型的空间复杂度,从而在有限的内存条件下处理长文本,Xia 等人 (2020) 提出了一种增量式的聚类算法:对于给定的文档,模型会预测出其中的描述片段,然后对于每一个描述片段,要么将其放入已有的某一个实体簇并更新簇表示,要么建立新的簇。
该方法的优点在于更符合人类增量阅读和推理相关描述的方式,毕竟没有人会真的去一一判断所有的实体描述对是否同指,我们更倾向于是记下已经出现的有限的几个实体簇,对于新出现的实体描述,要么将其放入已有的簇中,要么是另起一个新的簇。换句话说保持有限的记忆约束是一种在心理语言学上更合理的阅读和建模同指消解的方法 (Webster & Curran, 2014)。
具体地,算法会记录并保存一个实体簇列表,对于预测出的每个描述片段,会通过打分器评估其与所有实体簇同指的概率,将问题从对实体-实体 (entity-entity) 打分转换为对实体-簇 (entity-cluster) 打分,如果判断其属于已有的某个簇,就将其信息融入到簇表示中(更新簇表示),或者建立新的簇:
建立空的实体簇列表 $E$
for $\text{segment} \in \text{Document}$ do
$M \leftarrow \text{Spans(segment)}$
for $m \in M$ do
$scores \leftarrow \text{PairScore}(m,E)$
$top_score \leftarrow \max(scores)$
$top_e \leftarrow \text{argmax}(scores)$
if $top_score > 0$ then
$\text{Update}(top_e,m)$
else
$\text{AddNewCluster}(E,m)$
return $E$
其中,$\text{Spans}()$ 负责返回候选描述片段,与前面的通用框架类似,采用一个描述打分器 $s_m(i)$ 对所有长度小于 $L$ 的片段都进行打分,然后只保留得分最高的前 $\lambda T$ 个片段;$\text{PairScore}()$ 是一个多层前馈神经网络,以描述表示和实体簇表示的拼接为输入,输出该描述属于对应簇的概率;$\text{Update}()$ 负责使用新加入的描述表示 $\boldsymbol{e}_m$ 来更新实体簇表示 $\boldsymbol{e}_{top\_e}$:
\[\begin{gather} \boldsymbol{\alpha} = \sigma(\text{FFNN}([\boldsymbol{e}_{top\_e};\boldsymbol{e}_m]))\\ \boldsymbol{e}_{top\_e} \leftarrow \boldsymbol{\alpha}\circ\boldsymbol{e}_{top\_e} + (1-\boldsymbol{\alpha})\circ\boldsymbol{e}_m \end{gather} \tag{11}\]由于该方法是对描述片段和实体簇进行打分,因此训练时,对于每一个片段只考虑最相关的那个实体簇,而不会考虑其所有的前情。具体地,对于每一个描述 $m$,$scores$ 可以视作是一个概率分布 $P(e\mid m) \text{ for } e \in E$,其中 $E$ 是实体簇列表还包含了一个空簇 $\varepsilon$ 表示创建一个新的簇。算法的目标就是最大化 $P(e = e_{\text{gold}}\mid m)$,$e_{\text{gold}}$ 就是 $m$ 的最相关的实体簇,即最近的前情被分配到的簇。
实际上,描述之间的信息量差异也是干扰同指判断的重要原因之一,很多时候描述所在的句子(局部片段)无法提供足够的上下文信息,或者两个同指的实体由于描述的侧重点不同而生成差异很大的语义表示。而簇表示能够提供更全面的信息,因此将问题转换为对实体-簇 (entity-cluster) 打分在一定程度上可以缓解这个问题。
事件同指消解
事件同指消解在形式上与实体同指消解非常类似,都是需要从生文本中识别出实体/事件描述,然后将它们按照指代关系聚类成簇。最大的不同在于,实体描述只是词语或者短语,而事件描述是由触发词和论元组成的图结构,并且论元就是实体,这种结构上的差异造成事件同指判断的难度要明显超过实体,某些情况下,事件同指的判断甚至需要依赖于实体同指的结果来判断论元是否同指,如下图所示。
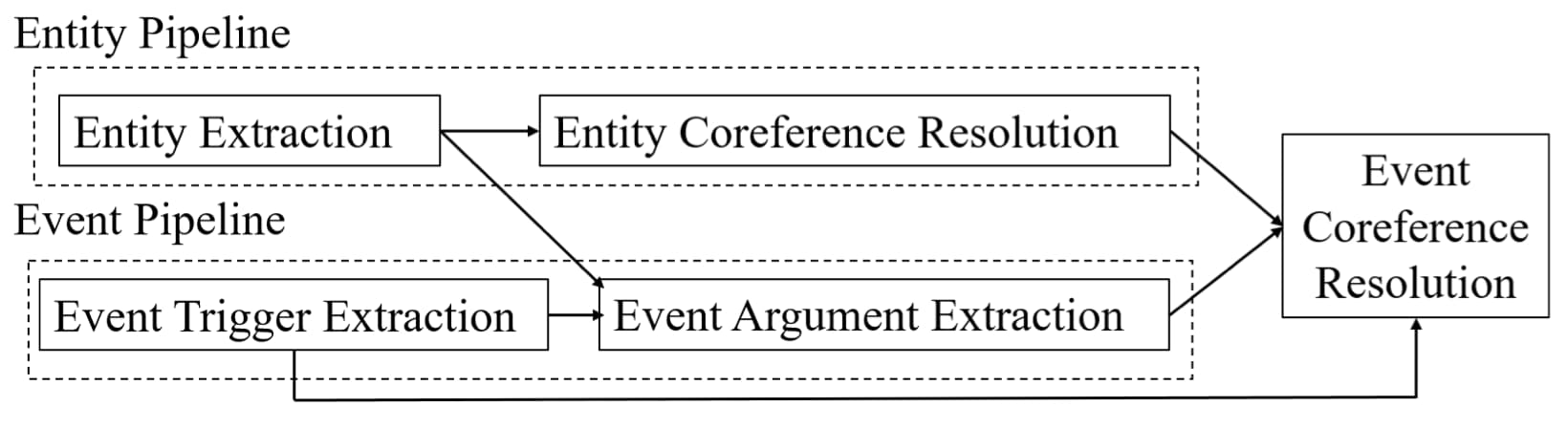
考虑到触发词是事件的核心,并且形式与实体一样只是词语或者短语,再加上论元识别、论元匹配、论元(实体)同指等步骤会引入额外的错误,因此大部分事件同指工作并不会去识别论元,而是直接将触发词作为事件描述。
也有少数工作探讨了论元(实体)指代对事件同指任务的帮助,后面会进行介绍。
有趣的是,与实体同指不同,目前大部分的事件同指工作依然采用管道 (pipeline) 模型,先识别出触发词,然后再判断同指关系,只有少部分工作采用了联合 (joint) 模型。并且根据 Lu 和 Ng (2021 EMNLP) 的分析显示,联合模型只有在同时进行多个额外任务时才会优于管道模型,如果只进行触发词识别和事件同指,那么管道模型性能更优。
事件同指联合框架
为了缓解由触发词识别带来的级联错误,也有部分工作 (Chen & Ng, 2016; Lu et al., 2016; Lu & Ng, 2017) 采用联合模型来进行事件同指消解。2021 年,Lu 和 Ng (2021 AAAI) 提出了第一个完全基于神经网络的联合模型,将端到端通用框架从实体同指任务迁移到事件同指任务中来。
\[s(i,j) = \begin{cases} 0 & j=\epsilon \\ s_m(i) + s_m(j) + s_a(i,j) & j \neq \epsilon \end{cases} \\ \begin{align} s_m(i) &= \boldsymbol{w}_m \cdot \text{FFNN}_m(\boldsymbol{g}_i)\\ s_a(i,j) &=\boldsymbol{w}_a \cdot \text{FFNN}_a([\boldsymbol{g}_i, \boldsymbol{g}_j,\boldsymbol{g}_i \circ \boldsymbol{g}_j,\phi(i,j)]) \end{align}\]事件同指模型同样采用式 $(2)$ 和 $(3)$,通过判断每一个片段 $i$ 为触发词的描述得分 $s_m(i)$ 和判断片段 $j$ 为片段 $i$ 的前情的 pairwise 得分 $s_a(i,j)$ 来计算片段 $i$ 和片段 $j$ 的 pairwise 同指分数 $s(i,j)$,同样采用裁剪方法 (pruning method) 来减小空间复杂度。特别地,对于每一个片段 $i$,还会通过一个前馈网络来判断其事件类型 (event subtypes)(包括 None,表示非触发词)$\boldsymbol{t}_i = \text{FFNN}_t(\boldsymbol{g}_i)$。
为了利用论元(实体)同指信息来辅助事件同指任务,事件同指联合框架联合地训练一个实体同指模型和一个事件同指模型,并且它们采用完全相同的模型结构,如下图所示:
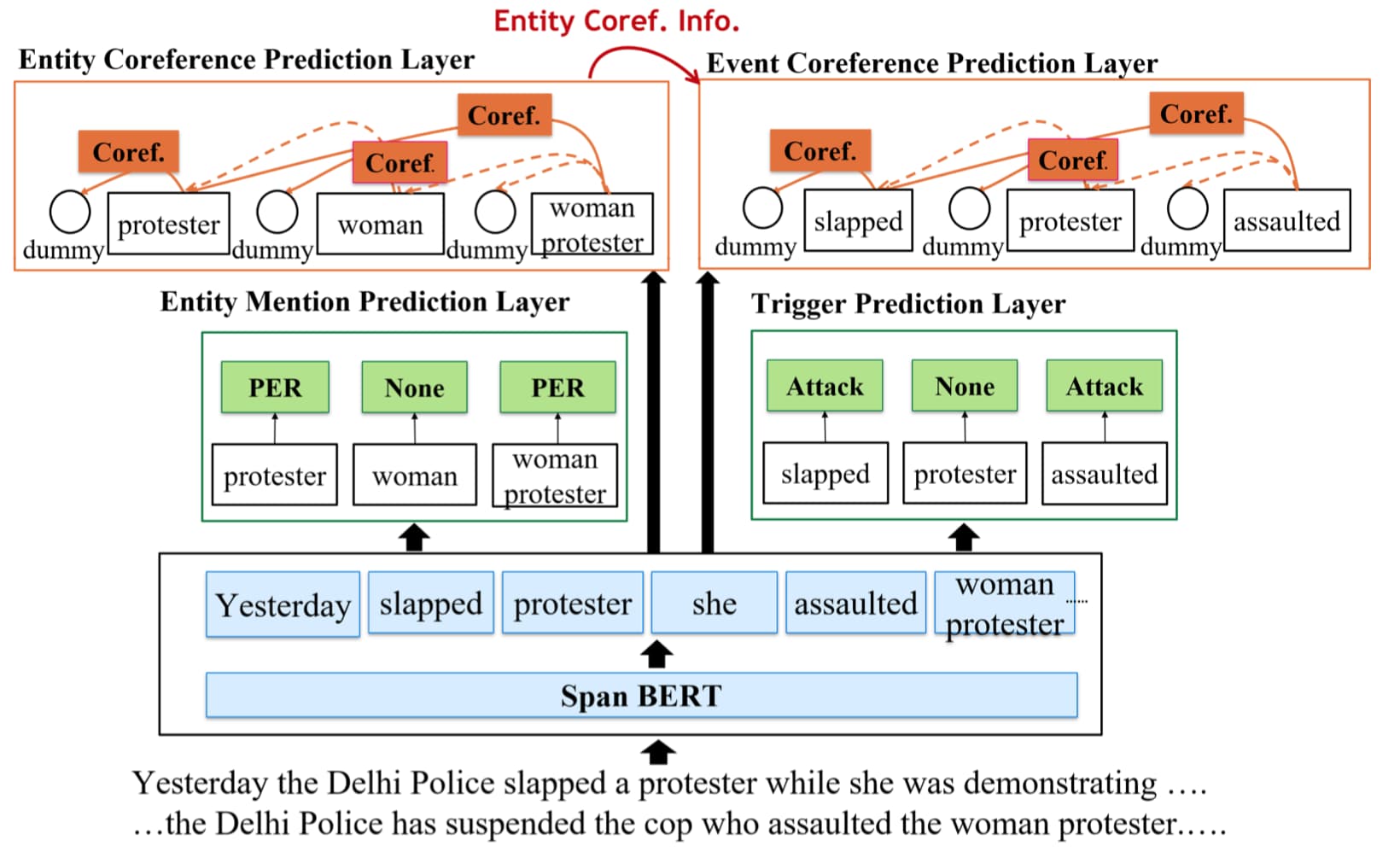
实体同指模型和事件同指模型除了共享编码器进行交互以外,还会显式地通过下面两种方法来融合实体同指信息用于事件同指:
-
硬约束 (hard constraint):如果两个事件描述的对应论元是非实体同指 (entity-coreferent) 的,那么它们就不能同指。无论是训练还是测试时,对于每个片段 $i$,都会先过滤掉违反该规则的候选前情。
要实现该约束,需要首先识别出事件描述的论元,并且判别它们对应的论元角色 (role)。一种简单的处理方法就是将与触发词依存路径 (dependency path) 长度短于 4 的所有实体都作为该事件描述的论元,并且将依存路径上的依存标签序列作为对应的论元角色。
-
直接作为特征:将实体同指信息转换为 2 个二元特征:
- 两个事件描述是否具有相同的论元角色;
- 是否它们的相同角色的论元是非实体同指的;
最终的实验结果证明,无论采用上面的哪一种方式,引入实体同指的信息都能够帮助提升事件同指的性能。
除了融入实体同指的信息以外,Lu 和 Ng (2021 NAACL) 还提出了一个联合学习 6 个任务的多任务框架,通过设计跨任务的连贯性约束 (cross-task consistency constraints) 来引导模型的学习。该工作可以看作是对上面框架的扩充,通过引入更多的额外相关信息来改进同指的性能。
除了联合建模以外,pipeline 模型也可以通过一些方法来缓解事件抽取带来的级联错误。例如 Lai 和 Ji (2021) 就提出了一种门控结构,它以触发词匹配信息为核心,对其他抽取出的 symbolic 特征进行过滤,挑选出与事件同指最相关的信息。
改进事件表示
由于事件是由触发词和论元组成,在结构上比实体更加复杂,因此如何建模生成更好的事件表示也是该领域的另一个研究重点。而且与实体同指任务类似,相比设计精巧的匹配方法与特征工程,生成更好的事件表示(表示学习)可能才是提升同指性能的关键。近年来许多工作 (Barhom et al., 2019) 都对该问题进行了探索:
-
论元匹配:许多早期的工作 (Chen et al., 2009; Cybulska & Vossen, 2015) 都将论元匹配作为判断事件同指的重要特征,但是无论是通过论元抽取和实体同指消解 (Chen & Ng, 2014, 2015; Lu & Ng, 2016),还是通过语义解析 (Peng et al., 2016; Choubey & Huang, 2017; Barhom et al., 2019),都会由于论元识别错误而引入噪声。为了解决这个问题,Huang 等人 (2019) 提出了一种迁移学习框架,通过大量无标注的数据来学习事件描述之间的论元匹配性 (argument compatibility),然后通过迁移学习将论元匹配性知识融入同指判断。除此以外,Zeng 等人 (2020) 跳过触发词-论元匹配,直接将识别出的语义角色标签作为 embeddings 拼接到语义表示的后面,然后再输入到 Transformer 编码器中获取最终的词语表示。
-
同指相关表示:在通过编码器获取描述的语义表示之后,再送入专门设计的同指嵌入网络 (coreference embedding network) 来进一步获取描述的同指相关表示,使得同指的描述表示更接近,不同指的描述表示更远离。Kenyon-Dean 等人 (2018) 以及 Kriman 和 Ji (2021) 通过吸引力和排斥力损失 (attraction and repulsion loss) 来实现该表示学习。当然,也可以直接通过对比学习 (contrastive learning) 损失来实现,但是要注意,直接以表示的余弦值作为优化目标是不合适的,因为即使是不同指的描述,也可能因为具有类似的上下文而生成接近的表示,我们只需要同指的表示比不同指的更接近即可,例如与 CoSENT 模型一样,使用 Circle Loss。
-
图结构表示:考虑到事件天然地具有图结构,即以触发词为核心,通过角色边连接论元实体。而且近年来许多工作成功地将图卷积 GCN 网络从知识图谱领域迁移用于其他领域,因此 Tran 等人 (2021) 也进行了类似的尝试,通过建立文档结构图然后再应用 GCN 来生成更好的事件描述表示。
具体地,令文档 $D=\{w_1,w_2,…,w_N\}$ 中的事件描述集合为 $E=\{e_1,e_2,…,e_{|e|}\}$,实体描述集合为 $M=\{m_1,m_2,…,m_{|M|}\}$,文档结构图为 $\mathcal{G} = \{\mathcal{N},\mathcal{E}\}$。考虑到点集 $\mathcal{N}$ 需要包含所有与事件同指相关的对象,因此这里选择所有的上下文词语(即 $w_i$)、事件描述和实体描述作为结点:
\[\mathcal{N} = D \cup E \cup M = \{n_1,n_2,...,n_{|\mathcal{N}|}\}\]这里通过预训练好的模型分别对实体描述和事件描述进行抽取(包括进行实体同指)。由于建立图结构需要预先识别出文档中的事件和实体,因此不可避免地存在级联错误。
文档结构图中的边负责控制结点之间的信息交互,这里考虑三种类型的边(基于篇章结构、基于依存树、基于语义相似度):
-
基于篇章结构的边:用于记录描述在文档 $D$ 中的位置以及彼此之间的依赖关系,具体又可以细分为:
- 句子边界:在同一个句子中的实体/事件描述相关性更强。对于结点 $n_i$ 和 $n_j$,计算它们的句子边界交互分数 $a_{ij}^{sent}$,如果 $n_i$ 和 $n_j$ 是同一个句子中的实体/事件描述($n_i,n_j \in E \cup M$),则 $a_{ij}^{sent} = 1$,否则为 $0$;
- 实体同指:对于每一对 $n_i$ 和 $n_j$,如果它们是同指的实体描述,那么 $a_{ij}^{coref}=1$,否则为 $0$;
- 描述片段:将实体/事件描述与上下文词语 $w_i$ 连接起来。如果 $n_i$ 是实体/事件描述片段 $n_j$ 中的词语($n_i \in D,n_j\in E \cup M$),那么 $a_{ij}^{span}=1$,否则为 $0$。
-
基于依存树的边:受先前工作 (Veyseh et al., 2020; Phung et al., 2021) 利用依存树来获取触发词和论元之间重要上下文信息的启发,可以首先通过语义角色识别 SRL 等方法识别触发词对应的论元(即保留 4 种语义角色 $Arg0,Arg1,Location,Time$),然后通过触发词和其所有论元 head 之间的最短依存路径来剪裁依存树,例如:
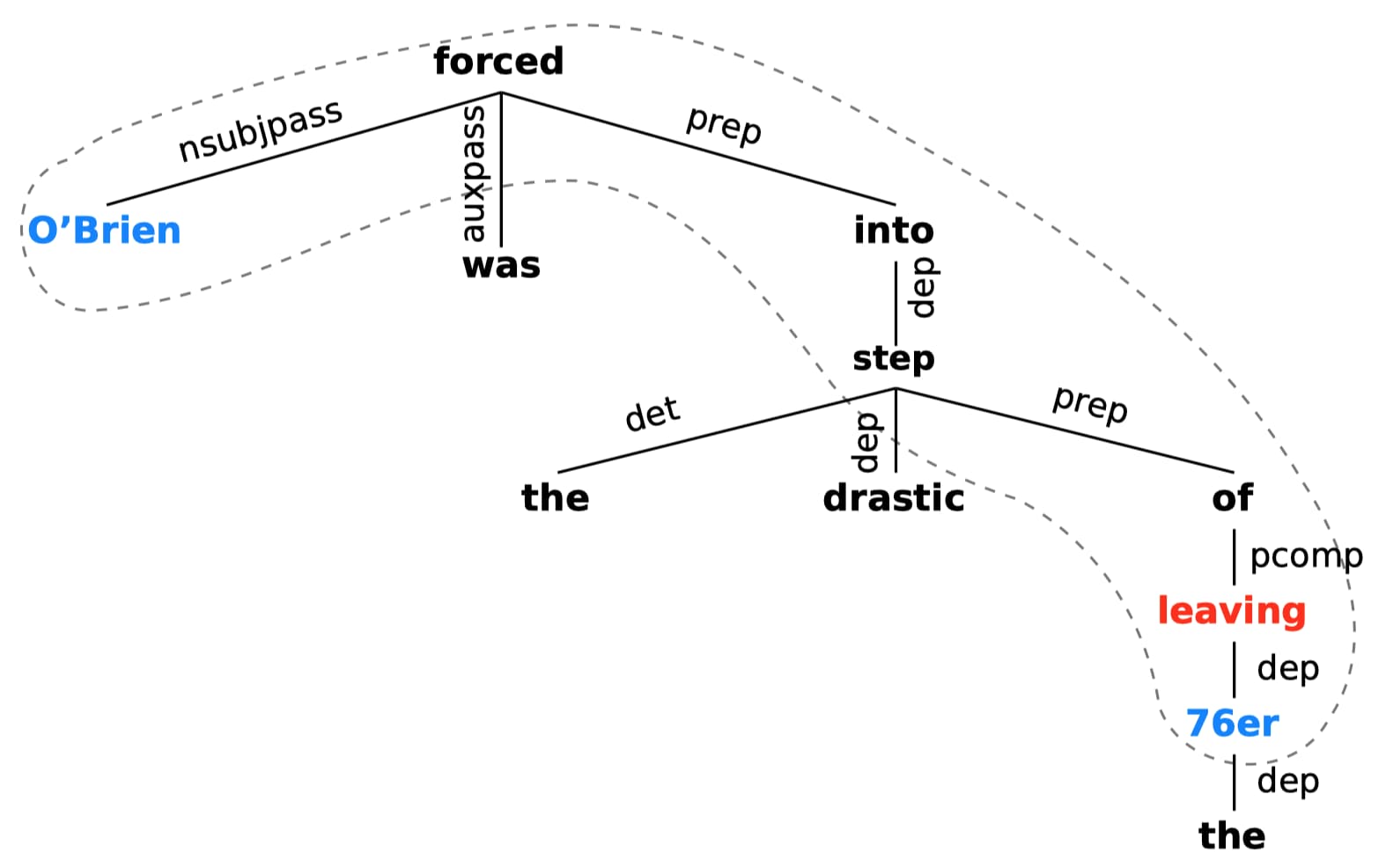
其中,红色的是触发词,蓝色的是论元的 head,虚线圈出的便是剪裁后的句法树。
或者只是简单地使用依存树来连接每一个句子中的词语,如果 $n_i$ 和 $n_j$ 是同一个句子中的两个词($n_i,n_j\in D$),并且在依存树中它们之间有边相连,那么 $a_{ij}^{dep} = 1$,否则为 $0$。
-
基于语义相似度的边:考虑到语义相似的节点可能更相关,使用语义相似度 $a_{ij}^{struct}$ 来连接词语节点。
最后,通过正则化合并上面的这些边,得到最终节点 $n_j$ 和 $n_j$ 之间的分数 $a_{ij}$(其中 $q$ 是维度为 5 的参数向量):
\[\begin{gather} d_{ij} = [a_{ij}^{sent},a_{ij}^{coref},a_{ij}^{span},a_{ij}^{dep},a_{ij}^{struct}]\\ a_{ij} = \exp(d_{ij}q^\top)/\sum_{u=1..|\mathcal{N}|}\exp(d_{iu}q^\top) \end{gather}\] -
迭代聚类算法
2019 年,Barhom 等人提出了一种迭代聚类算法(Phung et al., 2021 对该模型进行了扩展),巧妙地通过每一轮迭代时形成的实体/事件聚类簇来改进实体和事件表示,即允许模型依据描述相关的论元或触发词的当前簇信息来辅助判别描述之间的同指关系,从而生成更好的实体/事件簇。
具体地,将文档 $D$ 中的实体描述和事件描述集合分别记为 $M^E$ 和 $M^V$,初始实体簇 $E^0$ 通过 CoreNLP 等工具识别建立,初始事件簇 $V^0$ 就是独立的事件描述。算法通过迭代生成新的实体簇 $E^k$ 和事件簇 $V^k$:
$E^0 \leftarrow$ 实体簇
$V^0 \leftarrow $ $M^V$ 中的独立事件描述
$k \leftarrow 1$
while $\exists \text{ meaningful cluster-pair merge}$ do
//实体
为所有的 $m_{e_i} \in M^E$ 生成新的实体表示 $R_E(m_{e_i},V^{k-1})$
计算实体描述对的同指分数 $S_E(m_{e_i},m_{e_j})$
使用 gold 实体簇训练 $R_E$ 和 $S_E$
$E^k \leftarrow$ 基于 $S_E(m_{e_i},m_{e_j})$ 聚类 $M^E$
//事件
为所有的 $m_{v_i} \in M^V$ 生成新的事件表示 $R_V(m_{v_i},E^{k})$
计算事件描述对的同指分数 $S_V(m_{v_i},m_{v_j})$
使用 gold 事件簇训练 $R_V$ 和 $S_V$
$V^k \leftarrow$ 基于 $S_V(m_{v_i},m_{v_j})$ 聚类 $M^V$
$k \leftarrow k + 1$
end while
其中,每一轮迭代中的聚类通过同样以初始簇 $E^0$ 和 $V^0$ 开始,贪心地合并具有最高聚类分数的多个簇,直到所有聚类分数都低于某一个阈值。簇 $c_i$ 和 $c_j$ 的聚类分数 $S_C(c_i,c_j)$ 通过簇中描述之间的同指分数来计算 (Barhom et al., 2019),$*$ 可以是 $E$ 或 $V$,取决于 $c_i,c_j$ 是实体簇或者事件簇:
\[S_C(c_i,c_j) = \frac{1}{|c_i||c_j|} \sum_{m_i \in c_i,m_i \in c_j} S_*(m_i,m_j)\]该算法的核心思想是:在第 $k$ 轮迭代时,首先根据当前的事件簇 $V^{k-1}$ 来更新实体表示 $R_E(m_{e_i},V^{k-1})$,从而聚类生成新的实体簇 $E^k$,然后又根据新预测出的实体簇 $E^k$ 来更新事件表示 $R_V(m_{v_i},E^{k})$,从而聚类生成新的事件簇 $V^k$。即通过不断迭代改进实体描述和事件描述的语义表示,从而生成更好的实体/事件簇。
重打分算法
除了前面介绍的增量聚类算法是计算描述-簇 (mantion-cluster) 得分以外,其余所有的方法都需要先计算描述对 (mantion-pair) 之间的同指得分,再基于这些得分构建同指簇。考虑到局部的描述对得分可能在全局层面存在矛盾,因此前面的工作通过高层推理、在 pairwise 打分器损失中加入一致性约束、对打分结果进行后处理等来缓解这个问题。其中 Ors 等 (2020) 提出的重打分 (Re-scoring) 算法可以看作是后处理技术的典型代表。
重打分算法的想法非常简单:对于任何一对描述 $m_i$ 和 $m_j$,都可以利用它们与其他描述 $m_k$ 的同指判别结果 $Coref(m_i,m_k)$ 和 $Coref(m_j,m_k)$ 来对它们的同指得分 $Score(m_i,m_j)$ 进行调整,如果对于大部分描述 $m_k$ 都可以得到相同的同指判断,那么 $m_i$ 和 $m_j$ 同指的概率就更高:
$All_Scores \leftarrow []$
$Mentions \leftarrow$ 文档中所有的描述
for $m_i$ in $Mentions$ do
for $m_j$ in $Mentions$ where $m_j \neq m_i$ do
if $Coref(m_i,m_j)=1$ then $Score(m_i,m_j)\leftarrow 1$
else $Score(m_i,m_j)\leftarrow -1$
end if
for $m_k$ in $Mention$ where $m_k \neq (m_i \text{ or } m_j)$ do
if $Coref(m_i, m_k) = 1$ and $Coref(m_j, m_k) = 1$ then
$Score(s_i, s_j) \leftarrow Score(s_i, s_j) + reward$
else if $Coref(m_i,m_k)\neq Coref(m_j,m_k)$ then
$Score(s_i,s_j) \leftarrow Score(s_i,s_j) - penalty$
end if
end for
$\text{INSERT } Score(s_i, s_j) \text{ into } All_Scores$
end for
end for
其中,奖励值 $reward$ 和惩罚值 $penalty$ 可以被设定为 $0 \sim 1$ 之间的数值。在对所有描述对完成重打分后,就可以按照同指得分和描述索引对描述对进行降序排列(只保留得分高于 $0$ 的),然后运用聚类算法生成最终的同指簇。
参考
[1] Lee et al., 2017 EMNLP. End-to-end Neural Coreference Resolution. Code (TensorFlow).
[2] Lee et al., 2018 NAACL-HLT. Higher-order Coreference Resolution with Coarse-to-fine Inference. Code (TensorFlow).
[3] Fei et al., 2019 ACL. End-to-end deep reinforcement learning based coreference resolution.
[4] Joshi et al., 2019 EMNLP-IJCNLP. BERT for coreference resolution: Baselines and analysis. Code (TensorFlow).
[5] Joshi et al., 2020 TACL. SpanBERT: Improving Pre-training by Representing and Predicting Spans. Code (PyTorch).
[6] Fernandes et al., 2012 CoNLL. Latent structure perceptron with feature induction for unrestricted coreference resolution.
[7] Martschat & Strube, 2015 TACL. Latent structures for coreference resolution.
[8] Kantor & Globerson, 2019 ACL. Coreference resolution with entity equalization. Code (TensorFlow).
[9] Xu & Choi, 2020 EMNLP. Revealing the Myth of Higher-Order Inference in Coreference Resolution. Code (PyTorch).
[10] Kirstain et al., 2021 ACL. Coreference Resolution without Span Representations. Code (PyTorch).
[11] Xia et al., 2020 EMNLP. Incremental Neural Coreference Resolution in Constant Memory. Code (Pytorch)
[12] Webster & Curran, 2014 COLING. Limited memory incremental coreference resolution.
[13] Wu et al., 2020 ACL. CorefQA: Coreference Resolution as Query-based Span Prediction. Code (TensorFlow)
[14] Lu & Ng, 2021 EMNLP. Conundrums in Event Coreference Resolution: Making Sense of the State of the Art.
[15] Chen & Ng, 2016 AAAI. Joint Inference over a Lightly Supervised Information Extraction Pipeline: Towards Event Coreference Resolution for Resource-Scarce Languages.
[16] Lu et al., 2016 COLING. Joint Inference for Event Coreference Resolution.
[17] Lu & Ng, 2017 ACL. Joint Learning for Event Coreference Resolution.
[18] Lu & Ng, 2021 AAAI. Span-Based Event Coreference Resolution.
[19] Lai & Ji, 2021 NAACL. A Context-Dependent Gated Module for Incorporating Symbolic Semantics into Event Coreference Resolution. Code (Pytorch)
[20] Kriman & Ji, 2021 ACL-IJCNLP. Joint Detection and Coreference Resolution of Entities and Events with Document-level Context Aggregation. Code (Pytorch)
[21] Lu & Ng, 2021 NAACL. Constrained Multi-Task Learning for Event Coreference Resolution.
[22] Chen et al., 2009 WS. A Pairwise Event Coreference Model, Feature Impact and Evaluation for Event Coreference Resolution.
[23] Cybulska & Vossen, 2015 EVENTS. Translating granularity of event slots into features for event coreference resolution.
[24] Chen & Ng, 2014 LREC. SinoCoreferencer: An end-to-end Chinese event coreference resolver.
[25] Chen & Ng, 2015 NAACL. Chinese Event Coreference Resolution: An Unsupervised Probabilistic Model Rivaling Supervised Resolvers.
[26] Lu & Ng, 2016 LREC. Event Coreference Resolution with Multi-Pass Sieves.
[27] Peng et al., 2016 EMNLP. Event Detection and Co-reference with Minimal Supervision.
[28] Huang et al., 2019 NAACL-HLT. Improving Event Coreference Resolution by Learning Argument Compatibility from Unlabeled Data.
[29] Veyseh et al., 2020 EMNLP. Graph transformer networks with syntactic and semantic structures for event argument extraction.
[30] Tran et al., 2021 ACL-IJCNLP. Exploiting Document Structures and Cluster Consistencies for Event Coreference Resolution.
[31] Barhom et al., 2019 ACL. Revisiting joint modeling of cross-document entity and event coreference resolution.
[32] Phung et al., 2021 NAACL-TextGraphs. Hierarchical Graph Convolutional Networks for Jointly Resolving Cross-document Coreference of Entity and Event Mentions.
[33] Choubey & Huang, 2017 EMNLP. Event coreference resolution by iteratively unfolding interdependencies among events.
[34] Zeng et al., 2020 COLING. Event Coreference Resolution with their Paraphrases and Argument-aware Embeddings.
[35] Ors et al., 2020 AESPEN. Event Clustering within News Articles.
[36] Kenyon-Dean et al., 2018 *SEM. Resolving Event Coreference with Supervised Representation Learning and Clustering-Oriented Regularization.
[37] Wang et al., 2021ACL-IJCNLP. CLEVE: Contrastive Pre-training for Event Extraction. Code (Pytorch).
[38] Guan et al., 2021 arXiv. What is Event Knowledge Graph: A Survey.