HMM 隐马尔可夫模型（下）：使用 Viterbi 算法寻找隐藏状态

在上一篇《HMM 隐马尔可夫模型（上）》中，我们通过一个掷骰子的例子，简单地阐述了一下 HMM 的基本概念，以及 HMM 关注问题的解决方法。文本将正式介绍隐马尔可夫模型的数学定义，并通过一个实例，演示具体问题的求解过程。

隐马尔可夫模型

隐马尔可夫模型中的变量可分为两组。第一组是状态变量 ${y_1,y_2,\cdots,y_n}$，其中 $y_i\in Y$ 表示第 $i$ 时刻的系统状态。通常假定状态变量是隐藏的、不可被观测的，因此状态变量亦称隐变量(hidden variable)。第二组是观测变量 ${x_1,x_2,\cdots,x_n}$，其中 $x_i \in X$ 表示第 $i$ 时刻的观测值。在隐马尔可夫模型中，系统通常在多个状态 ${s_1,s_2,\cdots,s_N}$ 之间转换，因此状态变量 $y_i$ 的取值范围 $Y$ (称为状态空间)通常是有 $N$ 个可能取值的离散空间。观测变量 $x_i$ 可以是离散型也可以是连续型。为方便讨论，我们仅考虑离散型观测变量，并假定其取值范围 $X$ 为 ${o_1,o_2,\cdots,o_M}$。隐马尔可夫模型的图结构如下所示：

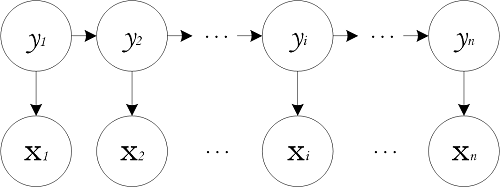
图中的箭头表示了变量间的依赖关系。在任一时刻，观测变量的取值仅依赖于状态变量，即 $x_t$ 由 $y_t$ 确定，与其他状态变量及观测变量的取值无关。同时，$t$ 时刻的状态 $y_t$ 仅依赖于 $t-1$ 时刻的状态 $y_{t-1}$，与其余 $n-2$ 个状态无关。这就是所谓的马尔可夫链(Markov chain)，即：系统下一时刻的状态仅由当前状态决定，不依赖于以往的任何状态。基于这种依赖关系，所有变量的联合概率分布为：

从马尔可夫链到马尔可夫模型

隐马尔可夫模型其实并不是 19 世纪俄罗斯数学家马尔可夫(Andrey Markov)发明的，而是美国数学家鲍姆(Leonard E. Baum)等人在 20 世纪六七十年代发表的一系列论文中提出的，隐马尔可夫模型的训练方法(鲍姆-韦尔奇算法)也是以他的名字命名的。

到了 19 世纪，概率论的发展从对随机变量的研究发展到对随机过程的研究。但是，随机过程要比随机变量复杂得多。首先，在任一时刻 $t$，对应的状态 $s_t$ 都是随机的；第二，任一状态 $s_t$ 的取值都可能和周围其他状态相关。这样随机过程就有了两个维度的不确定性。马尔可夫为了简化问题，提出一种假设：随机过程中各个状态 $s_t$ 的概率分布只与它前一个状态 $s_{t-1}$ 有关，即 $P(s_t\mid s_1,s_2,\cdots,s_{t-1})=P(s_t\mid s_{t-1})$。这种假设未必适合所有的应用，但是至少对以前很多不好解决的问题给出了近似解。这个假设后来被命名为马尔可夫假设，又称马尔可夫链。

隐马尔可夫模型是马尔可夫链的一个扩展，其中隐含的状态序列是一个典型的马尔可夫链。鲍姆把这种模型称为“隐含”马尔可夫模型。

除了结构信息，欲确定一个隐马尔可夫模型还需以下三组参数：

• 状态转移概率：模型在各个状态间转换的概率，通常记为矩阵 $\mathbf{A}=[a_{ij}]_{N\times N}$，其中：

  \[a_{ij}=P(y_{t+1}=s_j\mid y_t=s_i),\quad1\le i,j\le N\]

  表示在任意时刻 $t$，若状态为 $s_i$，则在下一时刻状态为 $s_j$ 的概率。

• 输出观测概率：模型根据当前状态获得各个观测值的概率，通常记为矩阵 $\mathbf{B}=[b_{ij}]_{N\times M}$，其中

  \[b_{ij}=P(x_t=o_j\mid y_t=s_i),\quad1\le i\le N,1\le j\le M\]

  表示在任意时刻 $t$，若状态为 $s_i$，则观测值 $o_j$ 被获取的概率。

• 初始状态概率：模型在初始时刻各状态出现的概率，通常记为 $\boldsymbol{\pi}=(\pi_1,\pi_2,\cdots,\pi_N)$，其中：

  \[\pi_i=P(y_1=s_i),\quad1\le i\le N\]

  表示模型的初始状态为 $s_i$ 的概率。

通过指定状态空间 $Y$、观测空间 $X$ 和上述三组参数，就能确定一个隐马尔可夫模型，通常用其参数 $\lambda=[\mathbf{A},\mathbf{B},\boldsymbol{\pi}]$ 来指代。给定隐马尔可夫模型 $\lambda$，它按如下过程产生观测序列 ${x_1,x_2,\cdots,x_n}$：

1. 设置 $t = 1$，并根据初始状态概率 $\boldsymbol{\pi}$ 选择初始状态 $y_1$；
2. 根据状态 $y_t$ 和输出观测概率 $\mathbf{B}$ 选择观测变量取值 $x_t$；
3. 根据状态 $y_t$ 和状态转移矩阵 $\mathbf{A}$ 转移模型状态，即确定 $y_{t+1}$；
4. 若 $t<n$，设置 $t = t + 1$，并转到第 2 步，否则停止。

其中 $y_t\in{s_1,s_2,\cdots,s_N}$ 和 $x_t\in{o_1,o_2,\cdots,o_M}$ 分别为第 $t$ 时刻的状态和观测值。

在实际应用中，人们常关注隐马尔可夫模型的三个基本问题：

• 给定模型 $\lambda=[\mathbf{A},\mathbf{B},\boldsymbol{\pi}]$，如何有效计算其产生观测序列 $\mathbf{x}={x_1,x_2,\cdots,x_n}$ 的概率 $P(\mathbf{x}\mid \lambda)$？换言之，如何评估模型与观测序列之间的匹配程度？
• 给定模型 $\lambda=[\mathbf{A},\mathbf{B},\boldsymbol{\pi}]$ 和观测序列 $\mathbf{x}={x_1,x_2,\cdots,x_n}$，如何找到与此观测序列最匹配的状态序列 $\mathbf{y}={y_1,y_2,\cdots,y_n}$？换言之，如何根据观测序列推断出隐藏的模型状态？
• 给定观测序列 $\mathbf{x}={x_1,x_2,\cdots,x_n}$，如何调整模型参数 $\lambda=[\mathbf{A},\mathbf{B},\boldsymbol{\pi}]$ 使得该序列出现的概率 $P(\mathbf{x}\mid\lambda)$ 最大？换言之，如何训练模型使其能最好地描述观测数据？

上述问题在现实应用中非常重要。例如许多任务需根据以往的观测序列 ${x_1,x_2,\cdots,x_{n-1}}$ 来推测当前时刻最有可能的观测值 $x_n$，这可以转化为求取概率 $P(\mathbf{x}\mid\lambda)$，即上述第一个问题；在语音识别等任务中，观测值为语音信号，隐藏状态为文字，目标就是根据观测信号来推断最有可能的状态序列(即对应的文字)，即上述第二个问题呢；在大多数现实应用中，人工指定模型参数已变得越来越不行，如何根据训练样本学得最优的模型参数，恰是上述第三个问题。

使用 Viterbi 算法寻找隐藏状态

正如前面所说，HMM 有三个金典问题。下面我们对第二个问题（即已知模型参数，寻找最可能的能产生某一特定输出序列的隐含状态的序列）给出一个实例，并通过 Viterbi 算法解决。

维特比算法(Viterbi algorithm)是一种动态规划算法。它用于寻找最有可能产生观测事件序列的维特比路径——隐含状态序列，特别是在马尔可夫信息源上下文和隐马尔可夫模型中。维特比算法由安德鲁·维特比于 1967 年提出，用于在数字通信链路中解卷积以消除噪音。现今也被常常用于语音识别、关键字识别、计算语言学和生物信息学中。

假设我有一个住的很远的朋友，她根据每天的天气情况（雨天、晴天）来决定当天的活动（公园散步、购物及清理房间）。我对于她所住地方的天气情况并不了解，但是我知道总的趋势。这个朋友每天会在微博上发布她做的事：“我今天出去散步了”、“我今天去超市购物了”、“今天清理了房间”等等，我希望通过她每天发的微博来推断她所在地的天气情况。

可以把天气情况看成是一个马尔可夫链，其有两个状态“雨天”和“晴天”，但是我们无法直接观察，或者说它们是隐藏的。因为这个朋友会把每天的活动发在微博上，所以这些活动就是可见的观测数据。这整个系统就是一个隐马尔可夫模型。

因为我知道这个地区的总的天气趋势，并且平时知道你朋友会做的事情，所以这个隐马尔可夫模型的参数是已知的。例如，可以用 Python 语言写下来：

states = ('Rainy', 'Sunny') #状态
observations = ('walk', 'shop', 'clean') #观测值序列
#初始状态概率
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
#状态转移概率
transition_probability = {
    'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
    'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
}
#输出观测概率
emission_probability = {
    'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
    'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}

Viterbi 算法

假设状态变量 $y_i$ 的取值范围是一个有 $N$ 个可能取值的离散空间 ${s_1,s_2,\cdots,s_N}$，且初始状态 $y_1=s_i$ 的概率为 $\pi_i$，从状态 $s_i$ 到状态 $s_j$ 的转移概率为 $a_{ij}$。令观察到的输出序列为 $x_1,x_2,\cdots,x_T$。则产生观察结果的最有可能的状态序列 $y_1,y_2,\cdots,y_T$ 由递推关系给出：

此处 $V_{t,s_i}$ 代表的是观测结果可能对应的前 $t$ 个最终状态为 $s_i$ 的状态序列的最大概率。通过保存向后指针记住在第二个等式中选择的状态 $s_k$ 可以获得维特比路径。声明一个函数 $Ptr(s_i,t)$，当 $t>1$ 时返回计算 $V_{t,s_i}$ 时用到的上一状态 $s_j$；当 $t=1$ 时，返回 $s_i$。这样：

简单一点来说，在任意时刻 $t$，我们都要计算 $y_t$ 取每一个状态 $s_i$ 时的最大概率，并且要记录下使得 $s_i$ 概率最大的上一状态，以便反推获得维特比路径。

完整 Python 代码实现

首先，我们需要一个路径概率表来存储任意时刻 $t$，每一个状态 $s_i$ 对应的状态序列的最大概率。我们用 [{s1:prob, s2:prob, ...}, ...] 这样的结构来存储路径概率表，列表 $t$ 位置的字典存储 $t$ 时刻对应的各状态 $s_i$ 的最大概率。我们首先编写路径概率表的展示函数：

# 打印路径概率表
def print_dptable(V):
	print "    ",
	for i in range(len(V)): print "%7d" % i,
	print
 
	for state in V[0].keys():
		print "%.5s: " % state,
		for t in range(len(V)):
			print "%.7s" % ("%f" % V[t][state]),
		print

接下来我们编写核心的 Viterbi 算法函数：

def viterbi(obs, states, start_p, trans_p, emit_p):
	'''
	:param obs:观测序列
	:param states:状态
	:param start_p:初始状态概率
	:param trans_p:状态转移概率
	:param emit_p:输出观测概率
	:return:
	'''
	V = [] #路径概率列表
	path = {} #维特比路径
	#初始状态 (t = 0)
	V.append({}) #状态最大概率用字典表示
	for state in states:
		V[0][state] = start_p[state] * emit_p[state][obs[0]]
		path[state] = [state]
	#对 t > 0 跑一遍维特比算法
	for t in range(1, len(obs)):
		V.append({})
		newpath = {}
		for s in states:
			(prob, state) = max([(V[t-1][s0] * trans_p[s0][s], s0) for s0 in states])
			V[t][s] = prob * emit_p[s][obs[t]]
			newpath[s] = path[state] + [s]
		#不需要保留旧路径
		path = newpath
 
	print_dptable(V)
	prob, state = max([(V[-1][s], s) for s in states])
	return prob, path[state]

运用之前我们提供的 HMM 各项参数，我们可以测试一下上面编写的算法：

print viterbi(observations,states,start_probability,transition_probability,emission_probability)

输出：

           0       1       2
Rainy:  0.06000 0.03840 0.01344
Sunny:  0.24000 0.04320 0.00259
(0.01344, ['Sunny', 'Rainy', 'Rainy'])

参考

1. 周志华《机器学习》
2. 维基百科《隐马尔可夫模型》《维特比算法》
3. 码农场《HMM与分词、词性标注、命名实体识别》
4. 吴军《数学之美》