转载自《玩转Keras之seq2seq自动生成标题》和《seq2seq之双向解码》,作者:苏剑林,部分内容有修改。
所谓 seq2seq,就是指一般的序列到序列的转换任务,比如机器翻译、自动文摘等等,这种任务的特点是输入序列和输出序列是不对齐的,如果对齐的话,那么我们称之为序列标注,这就比 seq2seq 简单很多了。所以尽管序列标注任务也可以理解为序列到序列的转换,但我们在谈到 seq2seq 时,一般不包含序列标注。
要自己实现 seq2seq,关键是搞懂 seq2seq 的原理和架构,一旦弄清楚了,其实不管哪个框架实现起来都不复杂。早期有一个第三方实现的Keras的seq2seq库,现在作者也已经放弃更新了,也许就是觉得这么简单的事情没必要再建一个库了吧。可以参考的资料还有去年 Keras 官方博客中写的《A ten-minute introduction to sequence-to-sequence learning in Keras》。
seq2seq 可以做的事情非常多,本文挑选的是比较简单的根据文章内容生成标题(中文),也可以理解为自动摘要的一种。
seq2seq 简介
基本结构
假如原句子为 $X=(a,b,c,d,e,f)$,目标输出为 $Y=(P,Q,R,S,T)$,那么一个基本的 seq2seq 就如下图所示。
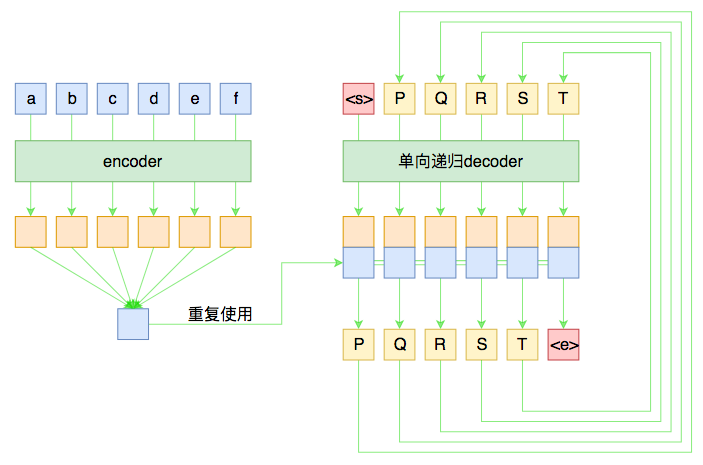
尽管整个图的线条比较多,可能有点眼花,但其实结构很简单。左边是对输入的 encoder,它负责把输入(可能是变长的)编码为一个固定大小的向量,这个可选择的模型就很多了,用 GRU、LSTM 等 RNN 结构或者 CNN+Pooling、Google 的纯 Attention 等都可以,这个固定大小的向量,理论上就包含了输入句子的全部信息。
而 decoder 负责将刚才我们编码出来的向量解码为我们期望的输出。与 encoder 不同,我们在图上强调 decoder 是“单向递归”的,因为解码过程是递归进行的,具体流程为:
- 所有输出端,都以一个通用的
<start>标记开头,以<end>标记结尾,这两个标记也视为一个词/字; - 将
<start>输入 decoder,然后得到隐藏层向量,将这个向量与 encoder 的输出混合,然后送入一个分类器,分类器的结果应当输出 $P$; - 将 $P$ 输入 decoder,得到新的隐藏层向量,再次与 encoder 的输出混合,送入分类器,分类器应输出 $Q$;
- 依此递归,直到分类器的结果输出
<end>。
这就是一个基本的 seq2seq 模型的解码过程,在解码的过程中,将每步的解码结果送入到下一步中去,直到输出 <end> 位置。
训练过程
事实上,上图也表明了一般的 seq2seq 的训练过程。由于训练的时候我们有标注数据对,因此我们能提前预知 decoder 每一步的输入和输出,因此整个结果实际上是“输入 $X$ 和 $Y_{\text{[:-1]}}$,预测 $Y_{\text{[1:]}}$,即将目标 $Y$ 错开一位来训练。这种训练方式,称之为 Teacher-Forcing。
而 decoder 同样可以用 GRU、LSTM 或 CNN 等结构,但注意再次强调这种“预知未来”的特性仅仅在训练中才有可能,在预测阶段是不存在的,因此 decoder 在执行每一步时,不能提前使用后面步的输入。所以,如果用 RNN 结构,一般都只使用单向 RNN;如果使用 CNN 或者纯 Attention,那么需要把后面的部分给 mask 掉(对于卷积来说,就是在卷积核上乘上一个 0/1 矩阵,使得卷积只能读取当前位置及其“左边”的输入,对于 Attention 来说也类似,不过是对 query 的序列进行 mask 处理)。
敏感的读者可能会察觉到,这种训练方案是“局部”的,事实上不够端到端。比如当我们预测 $R$ 时是假设 $Q$ 已知的,即 $Q$ 在前一步被成功预测,但这是不能直接得到保证的。一般前面某一步的预测出错,那么可能导致连锁反应,后面各步的训练和预测都没有意义了。
有学者考虑过这个问题,比如文章《Sequence-to-Sequence Learning as Beam-Search Optimization》把整个解码搜索过程也加入到训练过程,而且还是纯粹梯度下降的(不用强化学习),是非常值得借鉴的一种做法。不过局部训练的计算成本比较低,一般情况下我们都只是使用局部训练来训练 seq2seq。
beam search 束搜索
前面已经多次提到了解码过程,但还不完整。事实上,对于 seq2seq 来说,我们是在建模
\[p(\boldsymbol{Y}\vert\boldsymbol{X})=p(Y_1\vert\boldsymbol{X})p(Y_2\vert\boldsymbol{X},Y_1)p(Y_3\vert\boldsymbol{X},Y_1,Y_2)p(Y_4\vert\boldsymbol{X},Y_1,Y_2,Y_3)p(Y_5\vert\boldsymbol{X},Y_1,Y_2,Y_3,Y_4)\tag{1}\]显然在解码时,我们希望能找到最大概率的 $\boldsymbol{Y}$,那要怎么做呢?
如果在第一步 $p(Y_1\vert\boldsymbol{X})$ 时,直接选择最大概率的那个(我们期望是目标 $P$),然后代入第二步 $p(Y_2\vert\boldsymbol{X},Y_1)$,再次选择最大概率的 $Y_2$,依此类推,每一步都选择当前最大概率的输出,那么就称为贪心搜索,是一种最低成本的解码方案。但是要注意,这种方案得到的结果未必是最优的,假如第一步我们选择了概率不是最大的 $Y_1$,代入第二步时也许会得到非常大的条件概率 $p(Y_2\vert\boldsymbol{X},Y_1)$,从而两者的乘积会超过逐位取最大的算法。
然而,如果真的要枚举所有路径取最优,那计算量是大到难以接受的(这不是一个马尔可夫过程,动态规划也用不了)。因此,seq2seq 使用了一种折中的方法:beam search。
这种算法类似动态规划,但即使在能用动态规划的问题下,它还比动态规划要简单,它的思想是:在每步计算时,只保留当前最优的 $top_k$ 个候选结果。比如取 $top_k=3$,那么第一步时,我们只保留使得 $p(Y_1\vert\boldsymbol{X})$ 最大的前 3 个 $Y_1$,然后分别代入 $p(Y_2\vert\boldsymbol{X},Y_1)$,然后各取前三个 $Y_2$,这样一来我们就有 $3^2=9$ 个组合了,这时我们计算每一种组合的总概率,然后还是只保留前三个,依次递归,直到出现了第一个 <end>。显然,它本质上还属于贪心搜索的范畴,只不过贪心的过程中保留了更多的可能性,普通的贪心搜索相当于 $top_k=1$。
seq2seq 提升
前面所示的 seq2seq 模型是标准的,但它把整个输入编码为一个固定大小的向量,然后用这个向量解码,这意味着这个向量理论上能包含原来输入的所有信息,会对 encoder 和 decoder 有更高的要求,尤其在机器翻译等信息不变的任务上。因为这种模型相当于让我们“看了一遍中文后就直接写出对应的英文翻译”那样,要求有强大的记忆能力和解码能力,事实上普通人完全不必这样,我们还会反复翻看对比原文,这就导致了下面的两个技巧。
Attention
Attention 目前基本上已经是 seq2seq 模型的“标配”模块了,它的思想就是:每一步解码时,不仅仅要结合 encoder 编码出来的固定大小的向量(通读全文),还要往回查阅原来的每一个字词(精读局部),两者配合来决定当前步的输出。
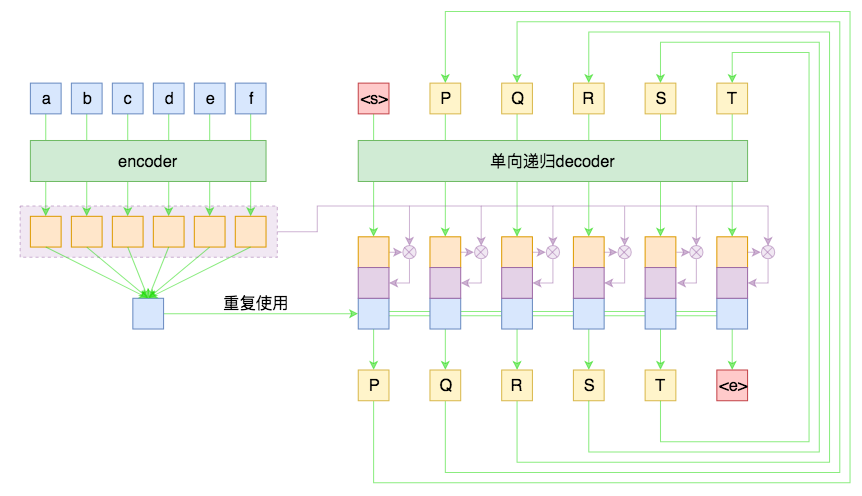
Attention 的具体做法可以参考《浅谈 NLP 中的 Attention 机制》。
先验知识
回到用 seq2seq 生成文章标题这个任务上,模型可以做些简化,并且可以引入一些先验知识。比如,由于输入语言和输出语言都是中文,因此 encoder 和 decoder 的 Embedding 层可以共享参数(也就是用同一套词向量)。这使得模型的参数量大幅度减少了。
此外,还有一个很有用的先验知识:标题中的大部分字词都在文章中出现过(注:仅仅是出现过,并不一定是连续出现,更不能说标题包含在文章中,不然就成为一个普通的序列标注问题了)。这样一来,我们可以用文章中的词集作为一个先验分布,加到解码过程的分类模型中,使得模型在解码输出时更倾向选用文章中已有的字词。
具体来说,在每一步预测时,我们得到总向量 $\boldsymbol{x}$(如前面所述,它应该是 decoder 当前的隐层向量、encoder 的编码向量、当前 decoder 与 encoder 的 Attention 编码三者的拼接),然后接入到全连接层,最终得到一个大小为 $\vert V\vert$ 的向量 $\boldsymbol{y}=(y_1,y_2,\dots,y_{\vert V\vert})$,其中 $\vert V\vert$ 是词表的词数。$\boldsymbol{y}$ 经过 softmax 后,得到原本的概率
\[p_i = \frac{e^{y_i}}{\sum_i e^{y_i}}\tag{2}\]这就是原始的分类方案。引入先验分布的方案是,对于每篇文章,我们得到一个大小为 $\vert V \vert$ 的 0/1 向量 $\boldsymbol{\chi}=(\chi_1,\chi_2,\dots,\chi_{\vert V\vert})$,其中 $\chi_i=1$ 意味着该词在文章中出现过,否则 $\chi_i=0$。将这样的一个 0/1 向量经过一个缩放平移层得到:
\[\hat{\boldsymbol{y}}=\boldsymbol{s}\otimes \boldsymbol{\chi} + \boldsymbol{t}=(s_1\chi_1+t_1, s_2\chi_2+t_2, \dots, s_{\vert V\vert}\chi_{\vert V\vert}+t_{\vert V\vert})\tag{3}\]其中 $\boldsymbol{s},\boldsymbol{t}$ 为训练参数,然后将这个向量与原来的 $\boldsymbol{y}$ 取平均后才做 softmax
\[\boldsymbol{y}\leftarrow \frac{\boldsymbol{y}+\hat{\boldsymbol{y}}}{2},\quad p_i = \frac{e^{y_i}}{\sum_i e^{y_i}}\tag{4}\]经实验,这个先验分布的引入,有助于加快收敛,生成更稳定的、质量更优的标题。
Keras 参考
又到了快乐的开源时光~
基本实现
基于上面的描述,我收集了 80 多万篇新闻的语料,来试图训练一个自动标题的模型。简单起见,我选择了以字为基本单位,并且引入了 4 个额外标记,分别代表 mask、unk、start、end。而 encoder 我使用了双层双向 LSTM,decoder 使用了双层单向 LSTM。具体细节可以参考源码:https://github.com/bojone/seq2seq/blob/master/seq2seq.py
我以 6.4 万文章为一个 epoch,训练了 50 个epoch(一个多小时)之后,基本就生成了看上去还行的标题:
文章内容:8月28日,网络爆料称,华住集团旗下连锁酒店用户数据疑似发生泄露。从卖家发布的内容看,数据包含华住旗下汉庭、禧玥、桔子、宜必思等10余个品牌酒店的住客信息。泄露的信息包括华住官网注册资料、酒店入住登记的身份 信息及酒店开房记录,住客姓名、手机号、邮箱、身份证号、登录账号密码等。卖家对这个约5亿条数据打包出售。第三方安全平台威胁猎人对信息出售者提供的三万条数据进行验证,认为数据真实性非常高。当天下午,华住集团发 声明称,已在内部迅速开展核查,并第一时间报警。当晚,上海警方消息称,接到华住集团报案,警方已经介入调查。
生成标题:《酒店用户数据疑似发生泄露》文章内容:新浪体育讯 北京时间10月16日,NBA中国赛广州站如约开打,火箭再次胜出,以95-85击败篮网。姚明渐入佳境,打了18分39秒,8投5中,拿下10分5个篮板,他还盖帽1次。火箭以两战皆胜的战绩圆满结束中国行。
生成标题:《直击:火箭两战皆胜火箭再胜 广州站姚明10分5板》
当然这只是两个比较好的例子,还有很多不好的例子,直接用到工程上肯定是不够的,还需要很多“黑科技”优化才行。
mask
在 seq2seq 中,做好 mask 是非常重要的,所谓 mask,就是要遮掩掉不应该读取到的信息、或者是无用的信息,一般是用 0/1 向量来乘掉它。
要注意我们以往一般是不区分 mask 和 unk(未登录词)的,但如果能把未登录词区分一下更好,因为未登录词尽管我们不清楚具体含义,它还是一个真正的词,至少有占位作用,而 mask 是我们希望完全抹掉的信息。
解码端
代码中已经实现了 beam search 解码,读者可以自行测试不同的 $top_k$ 对解码结果的影响。
这里要说的是,参考代码中对解码的实现是比较偷懒的,会使得解码速度大降。理论上来说,我们每次得到当前时刻的输出后,我们只需要传入到 LSTM 的下一步迭代中去,就可以得到下一时刻的输出,但这需要重写解码端的 LSTM(也就是要区分训练阶段和测试阶段,两者共享权重),相对复杂,而且对初学者并不友好。所以我使用了一个非常粗暴的方案:每一步预测都重跑一次整个模型,这样一来代码量最少,但是越到后面越慢,原来是 $\mathscr{O}(n)$ 的计算量变成了 $\mathscr{O}(n^2)$。
进一步提升:双向解码机制
下面我们将这个 seq2seq 再往前推一步,引入双向的解码机制,它在一定程度上能提高生成文本的质量(尤其是生成较长文本时)。
本文所介绍的双向解码机制参考自《Synchronous Bidirectional Neural Machine Translation》。
背景介绍
常见的 seq2seq 的解码过程是从左往右逐字(词)生成的,即根据 encoder 的结果先生成第一个字;然后根据 encoder 的结果以及已经生成的第一个字,来去生成第二个字;再根据 encoder 的结果和前两个字,来生成第三个词;依此类推。总的来说,就是在建模如下概率分解
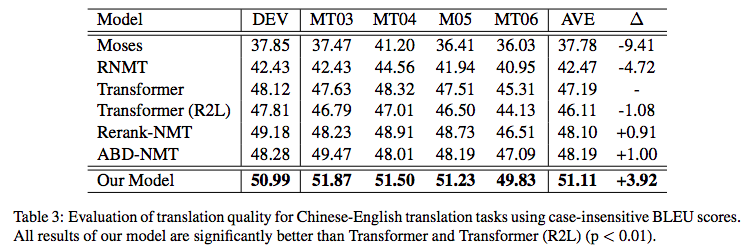
\[p(\boldsymbol{Y}\vert\boldsymbol{X})=p(Y_1\vert\boldsymbol{X})p(Y_2\vert\boldsymbol{X},Y_1)p(Y_3\vert\boldsymbol{X},Y_1,Y_2)\cdots \tag{5}\]当然,也可以从右往左生成,也就是先生成倒数第一个字,再生成倒数第二个字、倒数第三个字,等等。问题是,不管从哪个方向生成,都会有方向性倾斜的问题。比如,从左往右生成的话,前几个字的生成准确率肯定会比后几个字要高,反之亦然。在《Synchronous Bidirectional Neural Machine Translation》给出了如下的在机器翻译任务上的统计结果:
\[\begin{array}{|c|c|c|} \hline \text{Model} & \text{The first 4 tokens} & \text{The last 4 tokens}\\ \hline \text{L2R} & 40.21\% & 35.10\%\\ \hline \text{R2L} & 35.67\% & 39.47\%\\ \hline \end{array}\]$\text{L2R}$ 和 $\text{R2L}$ 分别是指从左往右和从右往左的解码生成。从表中我们可以看到,如果从左往右解码,那么前四个 token 的准确率有 40% 左右,但是最后 4 个token的准确率只有 35%;反过来也差不多。这就反映了解码的不对称性。
为了消除这种不对称性,《Synchronous Bidirectional Neural Machine Translation》提出了一个双向解码机制,它维护两个方向的解码器,然后通过 Attention 来进一步对齐生成。
双向解码
虽然本文参考自《Synchronous Bidirectional Neural Machine Translation》,但我没有完全精读原文,我只是凭自己的直觉粗读了原文,大致理解了原理之后自己实现的模型,所以并不保证跟原文完全一致。此外,这篇论文并不是第一篇做双向解码生成的论文,但它是我看到的双向解码的第一篇论文,所以我就只实现了它,并没有跟其他相关论文进行对比。
基本思路
既然叫双向“解码”,那么改动就只是在 decoder 那里,而不涉及到 encoder,所以下面的介绍中也只侧重描述 decoder 部分。还有,要注意的是双向解码只是一个策略,而下面只是一种参考实现,并不是标准的、唯一的,这就好比我们说的 seq2seq 也只是序列到序列生成模型的泛指,具体 encoder 和 decoder 怎么设计,有很多可调整的地方。
首先,给出一个简单的示意动图,来演示双向解码机制的设计和交互过程:
如图所示,双向解码基本上可以看成是两个不同方向的解码模块共存,为了便于描述,我们将上方称为 L2R 模块,而下方称为 R2L 模块。开始情况下,大家都输入一个起始标记(上图中的 S),然后 L2R 模块负责预测第一个字,而 R2L 模块负责预测最后一个字;接着,将第一个字(以及历史信息)传入到 L2R 模块中,来预测第二个字,为了预测第二个字,除了用到 L2R 模块本身的编码外,还用到 R2L 模块已有的编码结果;反之,将最后一个字(以及历史信息)传入到 R2L 模块,再加上L2R模块已有的编码信息,来预测倒数第二个字;依此类推,直到出现了结束标记(上图中的 E)。
数学描述
换句话说,每个模块预测每一个字时,除了用到模块内部的信息外,还用到另一模块已经编码好的信息序列,而这个“用”是通过 Attention 来实现的。用公式来说,假设当前情况下 L2R 模块要预测第 $n$ 个字,以及 R2L 模块要预测倒数第 $n$ 个字。假设经过若干层编码后,得到的 L2R 向量序列(对应图中左上方的第二行)为:
\[H^{(l2r)}=\left[h_1^{(l2r)},h_2^{(l2r)},\dots,h_n^{(l2r)}\right] \tag{6}\]而 R2L 的向量序列(对应图中左下方的倒数第二行)为:
\[H^{(r2l)}=\left[h_1^{(r2l)},h_2^{(r2l)},\dots,h_n^{(r2l)}\right] \tag{7}\]如果是单向解码的话,我们会用 $h_n^{(l2r)}$ 作为特征来预测第 $n$ 个字,或者用 $h_n^{(r2l)}$ 作为特征来预测倒数第 $n$ 个字。
在双向解码机制下,我们以 $h_n^{(l2r)}$ 为 query,然后以 $H^{(r2l)}$ 为 key 和 value 来做一个 Attention,用 Attention 的输出作为特征来预测第 $n$ 个字,这样在预测第 $n$ 个字的时候,就可以提前“感知”到后面的字了;同样地,我们以 $h_n^{(r2l)}$ 为 query,然后以 $H^{(l2r)}$ 为 key 和 value 来做一个 Attention,用 Attention 的输出作为特征来预测倒数第 $n$ 个字,这样在预测倒数第 $n$ 个字的时候,就可以提前“感知”到前面的字了。上面示意图中,上面两层和下面两层之间的交互,就是指 Attention。在下面的代码中,用到的是最普通的乘性 Attention(参考《浅谈 NLP 中的 Attention 机制》)。
模型实现
上面就是双向解码的基本原理和做法。可以感觉到,这样一来,seq2seq 的 decoder 也变得对称起来了,这是一个很漂亮的特点。当然,为了完全实现这个模型,还需要思考一些问题:
- 怎么训练?
- 怎么预测?
训练方案
跟普通的 seq2seq 一样,基本的训练方案就是用所谓的 Teacher-Forcing 的方式来进行训练,即 L2R 方向在预测第 $n$ 个字的时候,假设前 $n−1$ 个字都是准确知道的,而 R2L 方向在预测倒数第 $n$ 个字的时候,假设倒数第 $n−1,n−2,…,1$ 个字都是准确知道的。最终的 loss 是两个方向的逐字交叉熵的平均。
不过这样的训练方案实在是无可奈何之举,后面我们会分析它信息泄漏的弊端。
双向束搜索
现在讨论预测过程。
如果是常规的单向解码的 seq2seq,我们会使用 beam search(束搜索)的算法,给出概率尽可能大的序列。
到了双向解码这里,情况变得复杂了一些。我们依然用 beam search 的思路,但是同时缓存两个方向的 $top_k$ 结果,也就是说,L2R 和 R2L 两个方向各存 $top_k$ 条临时路径。此外,由于双向解码时,L2R 的解码是要参考 R2L 已有的解码结果的,所以当我们要预测下一个字时,除了要枚举概率最高的 $top_k$ 个字、枚举 $top_k$ 条 L2R 的临时路径外,还要枚举 $top_k$ 条 R2L 的临时路径,所以一共要计算 $top_k^3$ 那么多个组合。而计算完成后,采用了一种最简单的思路:对每种“字 - L2R 临时路径”的得分在“R2L 临时路径”这一维度上做了平均,使得的分数变回 $top_k^2$ 个,作为每种“字 - L2R 临时路径”的得分,再从这 $top_k^2$ 个组合中,选出分数最高的 $top_k$ 个。而 R2L 这边的解码,则要进行反向的、相同的处理。最后,如果 L2R 和 R2L 两个方向都解码出了完成的句子,那么就选择概率(得分)最高的那个。
这样的整个过程,我们称之为“双向束搜索(双向 beam search)”。如果读者自己比较熟悉单向的 beam search,甚至自己都写过 beam search 的话,上述过程其实不难理解(看看代码就更容易懂了),它算是单向 beam search 自然延伸。当然,如果对 beam search 本身不了解的话,看上述搜索的过程应该是云里雾里的。所以想要弄清楚原理的读者,应该要从常规的单向 beam search 出发,先把它弄懂了,然后再看上述解码过程的描述,最后再看看下面给出的参考代码,就容易弄懂了。
代码参考
下面是笔者给出了双向解码的参考实现,跟之前 Keras 参考一节一致,只是解码端从双向换成单向了:https://github.com/bojone/seq2seq/blob/master/seq2seq_bidecoder.py
在这个实现里,我觉得有必要解释一下起始标记和结束标记的事情。在之前的单向解码的例子中,笔者是用 2 作为起始标记,用 3 作为结束标记。到了双向解码这里,一个很自然的问题就是:L2R 和 R2L 两个方向是不是应该要用两套起始和结束标记呢?
其实这个应该没有什么标准答案,我觉得不管是共用一套还是维护两套起止标记,结果可能都差不多。至于我在上面的参考代码中,使用的方案有点另类,但我认为比较符合直觉,具体是:依然是只用一套,但是在 L2R 方向中,用 2 作为起始标记、3 作为结束标记,而在 R2L 方向中,用 3 作为起始标记、2 作为结束标记。
思考分析
最后,我们进一步思考一下这种双向解码方案。尽管将解码过程对称化是一个很漂亮的特点,但也不代表它完全没有问题了,将它思考得更深入一些,有助于我们更好地理解和使用它。
改进生成的原因
一个有意思的问题是:看上去双向解码确实能提高句子首尾的生成质量,但会不会同时降低中间部分的生成质量?
当然,理论上这是有可能的,但实际测试时不是很严重。一方面,seq2seq 架构的信息编码和解码能力还是很强的,所以不会轻易损失信息;另一方面,我们自己去评估一个句子的质量的时候,往往会重点关注首尾部分,如果首尾部分都很合理,而中间部分不至于太糟糕的话,那么我们都认为它是一个合理的句子;反过来,如果首或尾不合理的话,我们会觉得这个句子很糟糕。这样一来,把句子首尾的生成质量提高了,整体的生成质量也就提高了。
对应不上概率模型
对于单向解码,我们有清晰的概率解释,即在估计条件概率 $p(\boldsymbol{Y}\vert\boldsymbol{X})$。但是在双向解码的时候,我们发现压根儿不知道怎么对应上一个概率模型,换句话说,我们感觉我们是在算概率,感觉效果也有了,却不知道真正算得是啥,因为条件概率的条件依赖完全已经被打乱了。
当然,如果真的有实效的话,理论美感差点也无妨,我说的这一点只是理论审美的追求,大家见仁见智就好。
信息提前泄漏
所谓信息泄漏,指的是本来作为预测目标的标签被用来做输入了,从而导致训练阶段的 loss 虚低(或者准确率虚高)。
由于在双向解码中,L2R 端的解码要去读取 R2L 端已有的向量序列,而在训练阶段,为了预测 R2L 端的第 $n$ 个字,是需要传入前 $n−1$ 个字的,这样一来,越解码到后面,信息泄漏就越严重。如下图所示:
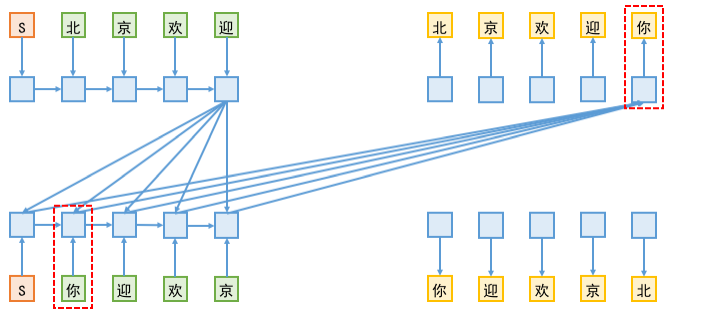
信息泄漏的一个表观现象是:训练到后期,双向解码中 L2R 和 R2L 两个方向的交叉熵之和,比单独训练单向解码模型时的单个交叉熵还要小,这并不是因为双向解码带来多大的拟合提升,而正是信息泄漏的体现。
既然训练过程中把信息泄漏了,那为什么这样的模型还有用呢?我想,大概的原因在文章一开头的表格中就给出了。还是刚才的例子,L2R 端在预测最后一个字“你”的时候,会用到了 R2L 端所有的已知信息;而 R2L 端是从右往左逐字解码的,按照文章一开头的表格的统计数据,我们不难想象到,对于 R2L 端来说,倒数第一个字的预测准确率应该是最高的。这样一来,假设 R2L 的倒数第一个字真的能以很高的准确率预测成功的话,那信息泄漏也变成不泄漏了———因为信息泄漏是因为我们人为地传入了标签,但如果预测的结果本身就跟标签一致,那泄漏也不再是泄漏了。
当然,原论文还提供了一个策略来缓解这个泄漏问题,大概做法是先用上述方式训练一版模型,然后对于每个训练样本,用模型生成对应的预测结果(伪标签),接着再去训练模型,这一次训练模型是传入伪标签来预测正确标签,这样就尽可能地保持了训练和预测的一致性。
转载自《玩转Keras之seq2seq自动生成标题》和《seq2seq之双向解码》,作者:苏剑林,部分内容有修改。