分类任务中的类别不平衡问题（上）：理论

什么是类别不平衡

大部分的分类模型都会假设不同类别的训练样例数目相当，但在实际运用中，经常会遇到不同类别的训练样例数目差别很大的情况（例如有 998 个负例，正例却只有 2 个），这时模型只需永远判定为数量最多的那个类别，就能达到很高的精度，这会对学习过程造成困扰。

分类任务中这种不同类别的训练样例数目差别很大的情况就被称为类别不平衡 (class imbalance)。不失一般性，下面都假定正例样本较少，负例样本较多。

再缩放

从线性分类器的角度很容易理解，在我们用 $y=\boldsymbol{w}^\top\boldsymbol{x}+b$ 对样本 $\boldsymbol{x}$ 进行分类时，实际上是在用预测出的 $y$ 与一个阈值进行比较，例如通常 $y \gt 0.5$ 判定为正例，否则为负例。$y$ 实际上表示正例的可能性，几率 $\frac{y}{1-y}$ 则表示正例可能性与负例可能性的比值，分类器决策规则为

\[\text{若 } \frac{y}{1-y}\gt 1 \text{ 则预测为正例} \tag{1}\]

阈值设为 $0.5$ 恰表明分类器认为真实正、负例可能性相同。但是，当训练集中样本类别不平衡时，令 $m^{+}$ 表示正例数目，$m^{-}$ 表示负例数量，则观测几率为 $\frac{m^{+}}{m^{-}}$。由于通常假设训练集是真实样本总体的无偏采样（真实样本总体的类别比例在训练集中得以保持），因此观测几率就代表了真实几率，只要分类器的预测几率高于观测几率就应判定为正例，即

\[\text{若 } \frac{y}{1-y} \gt \frac{m^{+}}{m^{-}} \text{ 则预测为正例} \tag{2}\]

但是阈值为 $0.5$ 时，分类器是基于 $(1)$ 进行决策的，因此需要对预测值进行调整，只需令

\[\frac{y'}{1-y'} = \frac{y}{1-y}\times\frac{m^{-}}{m^{+}} \tag{3}\]

这就是类别不平衡学习的一个基本策略——再缩放 (rescaling) 或再平衡 (rebalance)。

欠采样、过采样与阈值移动

但是在实际操作中，“训练集是真实样本总体的无偏采样”这个假设往往并不成立，我们无法有效地基于训练集观测几率来推断出真实几率，因此无法直接应用再缩放策略。目前，通常采用以下三种做法：

欠采样 (undersampling)，又称下采样 (downsampling)。对训练集中的负例样本进行“欠采样”，去除一些负例，使得正、负例数目接近，然后再进行学习；
过采样 (oversampling)，又称上采样 (upsampling)。对训练集中的正例样本进行“过采样”，增加一些正例，使得正、负例数目接近，然后再进行学习；
阈值移动 (threshold moving)，不改变训练集，在进行预测时，将式 $(3)$ 嵌入到决策过程中。

需要注意，过采样法不能简单地对初始正例样本进行重复采样，否则会招致严重的过拟合，代表性算法 SMOTE 是通过对训练集中的正例进行插值来产生额外的正例。同样地，欠采样法也不能随机丢弃负例，否则可能丢失一些重要信息，代表性算法 EasyEnsemble 则是利用集成学习机制，将负例划分为若干个集合供不同学习器使用，这样对每个学习器来看都进行了欠采样，但在全局来看不会丢失重要信息。

以 Cardio 数据集为例，共包含 1831 个样本，其中正例 176 个 (9.6122%)，负例 1655 个 (90.3878%)，属于典型的类别不平衡问题。下图展示了对原始数据分别采用欠采样、过采样和 SMOTE 采样法后的结果：

不同采样方法在 2 维空间上的展示（使用 T-SNE 嵌入到 2 维空间后）

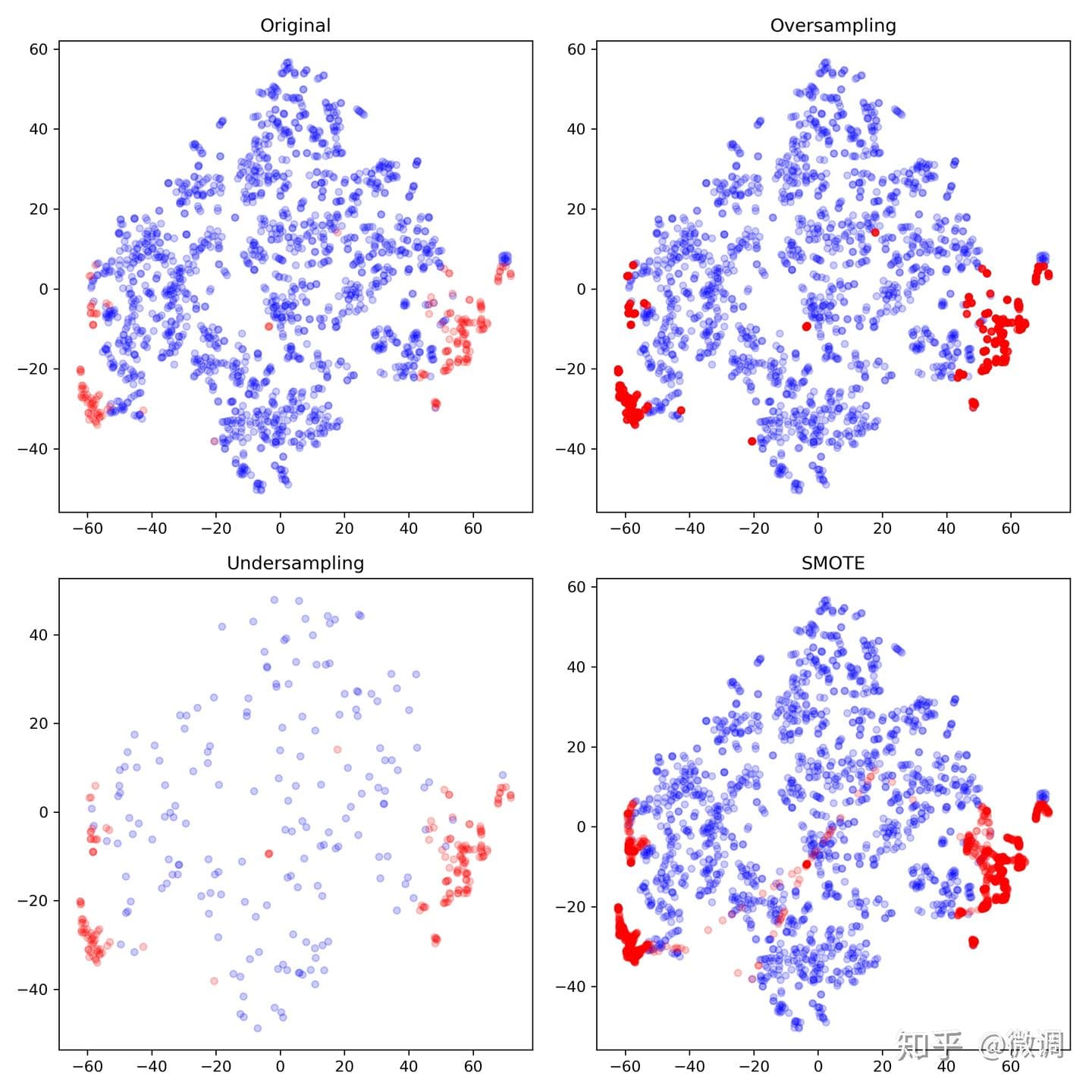
这里，欠采样法直接从负例中随机选择 176 个样本，与正例合并；过采样法从正例中反复抽取出 1655 个样本（势必会重复），并与负例合并。SMOTE 则通过找到正例中样本的近邻，来合成新的 1655-176=1479 个“新正例”，并与原始数据合并。

从图中可以看到：

过采样法（右上）只是单纯地重复了正例，如果其中部分点标记错误或者是噪音，那么错误也容易被成倍地放大，因此容易对正例过拟合；
欠采样（左下）抛弃了大部分负例数据，从而弱化了中间部分负例的影响，可能会造成偏差很大的模型；
SMOTE （右下）在局部区域通过 $K$-近邻生成了新的正例，一定程度上降低了过拟合风险，但是运算开销很大，而且在中间区域生成了一些“可疑的点”（中间的红点）。

常用的过采样法

SMOTE

如前面介绍的那样，SMOTE (synthetic minority oversampling technique) 的思想概括起来就是在正例样本之间进行插值来产生额外的样本。具体地，对于一个正例样本 $\boldsymbol{x}_i$，首先使用 $K$-近邻法找到距离最近的 $K$ 个正例样本（欧氏距离），然后从 $K$ 个近邻点中随机选取一个，使用下列公式生成新的正例样本：

\[\boldsymbol{x}_{new} = \boldsymbol{x}_i + (\hat{\boldsymbol{x}}_i - \boldsymbol{x}_i)\times \delta \tag{4}\]

其中 $\hat{\boldsymbol{x}}$ 为选出的 $K$ 近邻点，$\delta \in [0,1]$ 是一个随机数。下图就是一个 SMOTE 生成样本的例子，使用的是 3-近邻，可以看出 SMOTE 生成的样本一般就在 $\boldsymbol{x}_i$ 和 $\hat{\boldsymbol{x}}_i$ 相连的直线上：

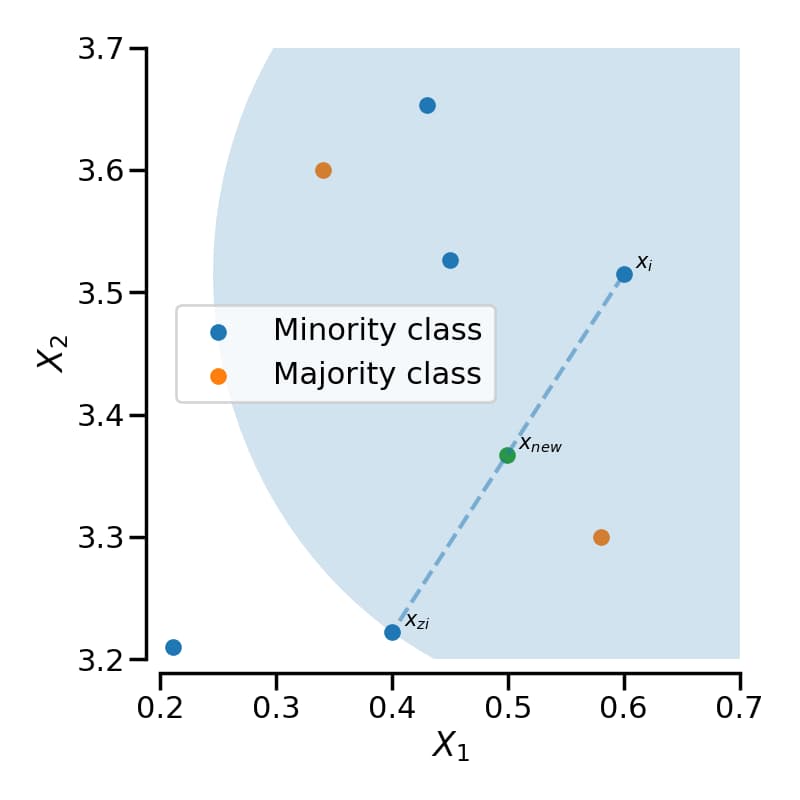
SMOTE 会随机选取正例样本用以合成新样本，而不考虑周边样本的情况，这样容易带来两个问题：

如果选取的正例样本周围也都是正例样本，则新合成的样本不会提供太多有用信息。这就像支持向量机中远离 margin 的点对决策边界影响不大。
如果选取的正例样本周围都是负例样本，这类的样本可能是噪音，则新合成的样本会与周围的负例样本产生重叠，致使分类困难。

因此，我们希望新合成的正例样本能处于两个类别的边界附近，这样往往能提供足够的信息用以分类。于是就有了 Border-line SMOTE 算法。Border-line SMOTE 算法会先将所有的正例样本分成三类：

noise：所有的 $K$ 近邻个样本都属于负例
danger：超过一半的 $K$ 近邻样本属于负例
safe：超过一半的 $K$ 近邻样本属于正例

Border-line SMOTE 算法只会从 danger 的正例样本中随机选择，然后用 SMOTE 算法产生新的样本。danger 样本代表靠近”边界“附近的正例样本，往往更容易被误分类，因而 Border-line SMOTE 只对那些靠近”边界“的正例样本进行人工合成样本。

Border-line SMOTE 又分为两种：Borderline-1 SMOTE 在合成样本时，$(4)$ 式中的 $\hat{\boldsymbol{x}}$ 是一个少数类样本；Borderline-2 SMOTE 中的 $\hat{\boldsymbol{x}}$ 则是 k 近邻中的任意一个样本。

ADASYN

与 SMOTE 直接对每个正例样本合成相同数量的样本不同，ADASYN (adaptive synthetic sampling) 首先通过算法计算出需要为每个正例样本产生多少合成样本，然后再用 SMOTE 算法合成新样本。具体来说，首先计算需要合成的正例样本总量 $G$：

\[G = (m^{-} - m^{+}) \times \beta \tag{5}\]

其中 $m^{-}$ 为负例样本的数量，$m^{+}$ 为正例样本的数量，$\beta \in [0,1]$ 为系数，如果 $\beta=1$ 则合成后各类别数目相等。然后，对于每个正例样本 $\boldsymbol{x}_i$，找出其 K 近邻个点，并计算：

\[\Gamma_i = \frac{\Delta_i\,/\,K}{Z} \tag{6}\]

其中 $\Delta_i$ 为 K 近邻个点中负例样本的数量，$Z$ 为规范化因子以确保 $\Gamma$ 构成一个分布。这样若一个正例样本 $\boldsymbol{x}_i$ 的周围负例样本越多，则其 $\Gamma_i$ 也就越高。

最后对每个正例样本 $\boldsymbol{x}_i$ 计算需要合成的样本数量 $g_i$，再用 SMOTE 算法合成新样本：

\[g_i = \Gamma_i \times G \tag{7}\]

可以看到，ADASYN 利用分布 $\Gamma$ 来自动决定每个正例样本所需要合成的样本数量，相当于给每个正例样本施加了一个权重，周围的负例样本越多则权重越高。因此 ADASYN 易受离群点的影响，如果一个正例样本的 K 近邻都是负例样本，则其权重会变得相当大，进而会在其周围生成较多的样本。

直观比较

为了直观地比较上面介绍的各种过采样法的效果，我们首先利用 sklearn中的 make_classification 构造了一个不平衡数据集，各类别比例为 ${0:54, 1:946}$。然后分别对这个数据集进行 SMOTEB、Borderline-1 SMOTEB、orderline-2 SMOTE 和 ADASYN 过采样结果如下图所示，左侧为过采样后的决策边界，右侧为过采样后的样本分布情况。

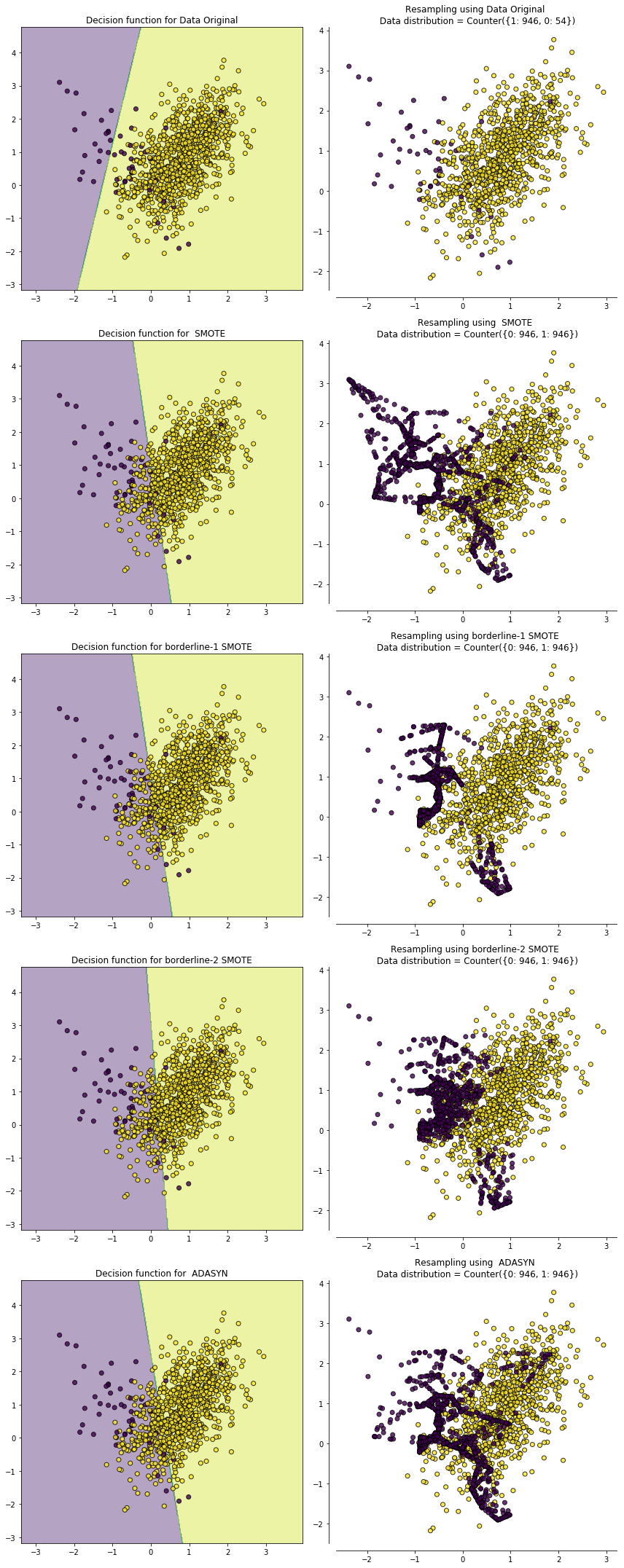
可以看到过采样后原来少数类的决策边界都扩大了，导致更多的负例样本被划为正例了。从上图我们也可以看出这几种过采样方法各自的特点：

用 SMOTE 合成的样本分布比较平均
Border-line SMOTE 合成的样本则集中在类别边界处。
ADASYN 的特性是一个正例样本周围负例样本越多，则算法会为其生成越多的样本，从图中也可以看到生成的样本大都来自于原来与负例比较靠近的那些正例样本。

常用的欠采样法

EasyEnsemble 和 BalanceCascade

如前面介绍的那样，EasyEnsemble 和 BalanceCascade 采用集成学习机制来处理随机欠采样中的信息丢失问题。

EasyEnsemble 将负例样本随机划分成 $n$ 个子集，每个子集的数量等于正例样本的数量，相当于欠采样。接着将每个子集与正例样本结合起来分别训练一个模型，最后将训练得到的 $n$ 个模型集成，这样集成后总信息量并不减少。如果说 EasyEnsemble 是基于无监督的方式从负例样本中生成子集进行欠采样，那么 BalanceCascade 则是采用了有监督结合 Boosting 的方式。

在 BalanceCascade 的第 $n$ 轮训练中，将从负例样本中抽样得来的子集与正例样本结合起来训练一个基学习器 $H$，训练完后负例中能被 $H$ 正确分类的样本会被剔除。在接下来的第 $n+1$ 轮中，从被剔除后的负例样本中产生子集用于与正例样本结合起来训练，最后将不同的基学习器集成起来。BalanceCascade 的有监督表现在每一轮的基学习器起到了在负例中选择样本的作用，而其 Boosting 特点则体现在每一轮丢弃被正确分类的样本，进而后续基学习器会更注重那些之前分类错误的样本。

NearMiss

NearMiss 本质上是一种原型选择 (prototype selection) 方法，即从负例样本中选取最具代表性的样本用于训练，从而缓解随机欠采样中的信息丢失问题。NearMiss 采用一些启发式的规则来选择样本：

NearMiss-1：选择到最近的 $K$ 个正例样本平均距离最近的负例样本；
NearMiss-2：选择到最远的 $K$ 个正例样本平均距离最近的负例样本；
NearMiss-3：对于每个正例样本选择 $K$ 个最近的负例样本，目的是保证每个正例样本都被负例样本包围。

为了更直观地对三种规则的采样效果进行展示，下图展示了分别采用 NearMiss-1、NearMiss-2 和 NearMiss-3 规则选择负例（多数类别）的结果。

NearMiss-1 和 NearMiss-2 的计算开销很大（需要计算每个负例样本的 $K$ 近邻点），此外 NearMiss-1 易受离群点的影响，如右上图中合理的情况是处于边界附近的多数类（负例）样本会被选中，然而由于右下方一些正例离群点的存在，其附近的多数类（负例）样本就被选择了。相比之下 NearMiss-2 和 NearMiss-3 不易产生这方面的问题。

数据清洗方法

数据清洗方法 (data cleaning tichniques) 主要通过规则来清洗重叠的数据，从而达到欠采样的目的，而这些规则往往也是启发性的，例如：

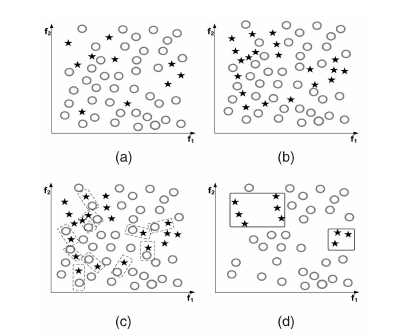
Tomek Link：Tomek Link 表示不同类别之间距离最近的一对样本，即两个样本互为最近邻且分属不同类别，那么要么其中一个是噪音，要么两个样本都在边界附近。这样通过移除 Tomek Link 就能“清洗掉”类间重叠样本，使得互为最近邻的样本皆属于同一类别，从而能更好地进行分类。

下图左上 $\text{(a)}$ 为原始数据，右上 $\text{(b)}$ 为 SMOTE 后的数据，左下 $\text{(c)}$ 虚线标识出 Tomek Link，右下为移除 Tomek Link 后的数据集，可以看到不同类别之间样本重叠减少了很多。
Edited Nearest Neighbours (ENN)：对于一个负例样本，如果其 $K$ 个近邻点有超过一半都是正例，则这个样本会被剔除。这个方法的另一个变种是如果所有的 $K$ 个近邻点都是正例，则这个样本会被剔除。

数据清洗技术最大的缺点是无法控制欠采样的数量。由于都在某种程度上采用了 $K$ 近邻法，而事实上大部分负例样本周围也都是负例，因而能剔除的负例样本比较有限。

结合过采样和欠采样

相信阅读到这里，一定有读者想问，既然过采样法和欠采样法都存在各自的缺点，那能不能将二者结合起来从而缓解问题呢？答案是肯定的。

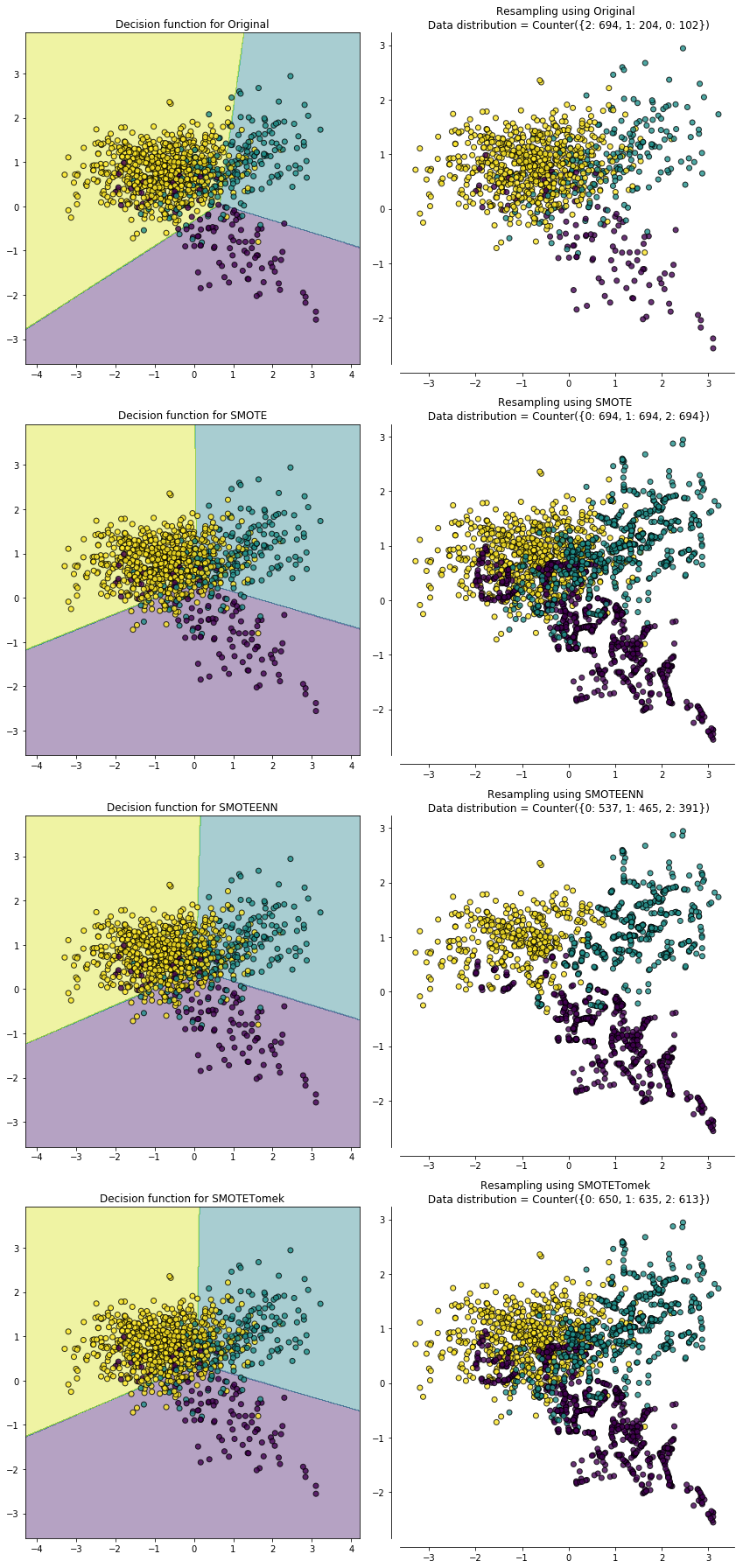
前面我们提到 SMOTE 算法的缺点是生成的正例样本容易与周围的负例样本产生重叠难以分类，而数据清洗技术恰好可以处理掉重叠样本，所以可以将二者结合起来形成一个 pipeline，先过采样再进行数据清洗。主要的方法是 SMOTE + ENN 和 SMOTE + Tomek ，其中 SMOTE + ENN 通常能清除更多的重叠样本，如下图：

提出这个结合过采样和欠采样方法的作者，还开发了一个专门用于处理数据不平衡的 Python 库——imbalanced-learn。除了我们介绍的这几种常用的过采样和欠采样的方法，其实还有更多的变种，读者如果感兴趣，可以参阅 imbalanced-learn 最后列出的 References。

在下一篇《分类任务中的类别不平衡问题（下）：实践》中，我们会亲自上手编写代码，使用 imbalanced-learn 库来进行实验。

参考

[1] 周志华《机器学习》
[2] 知乎. 欠采样（undersampling）和过采样（oversampling）会对模型带来怎样的影响？微调的回答
[3] 机器学习之类别不平衡问题 (3) —— 采样方法
[4] Jason Brownlee. Undersampling Algorithms for Imbalanced Classification

下篇使用 imbalanced-learn 库