Google 在论文《Transformer Quality in Linear Time》中提出了一种新的高效 Transformer 模型 FLASH-Quad,它虽然依旧具有二次复杂度,但是速度更快、显存占用更低、效果更好。
知名博主苏剑林对该设计进行了深度解读,并且在此基础上又进行了一些拓展思考。本文将简单梳理这几篇博文的核心内容,帮助大家快速了解该模型。
从 GLU 到 GAU
标准 Transformer 其实是 Attention 层和 FFN 层交替构建的,而 FLASH 模型的核心就是提出了一个融合了两者的门控注意力单元 GAU (Gated Attention Unit),它是新模型更快、更省、更好的关键。
我们都知道,标准的 FFN 是两层 MLP 模型:
\[\boldsymbol{O}=\phi(\boldsymbol{X}\boldsymbol{W}_u)\boldsymbol{W}_o\tag{1}\]这里 $\boldsymbol{X}\in\mathbb{R}^{n\times d},\boldsymbol{W}_u\in\mathbb{R}^{d\times e},\boldsymbol{W}_o\in\mathbb{R}^{e\times d}$,$\phi$ 是激活函数。后来,《GLU Variants Improve Transformer》发现使用了门控线性单元 GLU (Gated Linear Unit) 的 FFN 效果更好,并为后来的 mT5 所用,其形式为:
\[\boldsymbol{U}=\phi_u(\boldsymbol{X}\boldsymbol{W}_u),\quad\boldsymbol{V}=\phi_v(\boldsymbol{X}\boldsymbol{W}_v)\\\boldsymbol{O}=(\boldsymbol{U}\odot\boldsymbol{V})\boldsymbol{W}_o\tag{2}\]这里 $\boldsymbol{W}_u,\boldsymbol{W}_v\in\mathbb{R}^{d\times e}$,$\odot$ 是逐位对应相乘(Hadamard 积)。一般情况下的 GLU 是 $\boldsymbol{U}$ 不加激活函数而 $\boldsymbol{V}$ 加Sigmoid,但这篇论文中 $\boldsymbol{U},\boldsymbol{V}$ 都加了激活函数 Swish(也叫 SiLU,Sigmoid Linear Unit)。
虽然 GLU 很有效,但是它并不能取代 Attention,因为它的各个 token 之间没有进行交互,即矩阵 $\boldsymbol{U},\boldsymbol{V}$ 的每一行都是独立运算的。因此,一个自然的想法就是把 token 之间的联系补充到 $\boldsymbol{U},\boldsymbol{V}$ 上去,而为了体现出跟 Attetion 的结合,一个比较自然的设计就是:
\[\boldsymbol{O}=(\boldsymbol{U}\odot\boldsymbol{A}\boldsymbol{V})\boldsymbol{W}_o\label{eq:mix}\tag{3}\]其中 $\boldsymbol{A}\in\mathbb{R}^{n\times n}$ 是 Attention 矩阵,负责融合 token 之间的信息。这样输出的 $\boldsymbol{O}$ 就包含了 token 之间的交互,原则上可以取代 Attention。在式 $(3)$ 中,如果 $\boldsymbol{A}$ 等于单位阵 $\boldsymbol{I}$,那么它就是 GLU 式的 FFN;而如果 $\boldsymbol{U}$ 是全 1 矩阵,那么它就是普通的注意力机制,所以 $(3)$ 可以看作是 Attention 和 FFN 的一个简单而自然的融合。
由于 GLU 本身性能就很强,因此某种程度上可以弱化对 Attention 的依赖,因此原论文使用了如下的简化版 Attention 矩阵:
\[\boldsymbol{A}=\frac{1}{n}\text{relu}^2\left(\frac{\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}}{\sqrt{s}}\right)=\frac{1}{ns}\text{relu}^2\left(\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}\right),\quad \boldsymbol{Z}=\phi_z(\boldsymbol{X}\boldsymbol{W}_z)\label{eq:relu-att}\tag{4}\]这里 $\boldsymbol{W}_z\in\mathbb{R}^{d\times s}$,$s$ 即注意力的 head_size,文中取了 $s=128$,而 $\mathcal{Q},\mathcal{K}$ 是简单的仿射变换(像 Layer Norm 中的乘 $\gamma$ 加 $\beta$),$\text{relu}^2$ 则是 $\text{relu}$ 后再平方。
跟标准的 Scaled-Dot Self Attention 类似,这里的注意力矩阵还是 $\boldsymbol{Q},\boldsymbol{K}$ 的内积并除以维度的平方根,复杂度还是 $\mathscr{O}(n^2)$,不过这里简化了 $\boldsymbol{Q},\boldsymbol{K}$ 的来源变换,并且激活函数换用了 $\text{relu}^2$。最后的 $\frac{1}{n}$ 是简单的归一化因子,用以消除长度的影响。
这个设计的成功也表明,注意力机制中的 softmax 不是必须的,可以换成常规的激活函数加简单的归一化。
GAU 模型结构如下图所示:
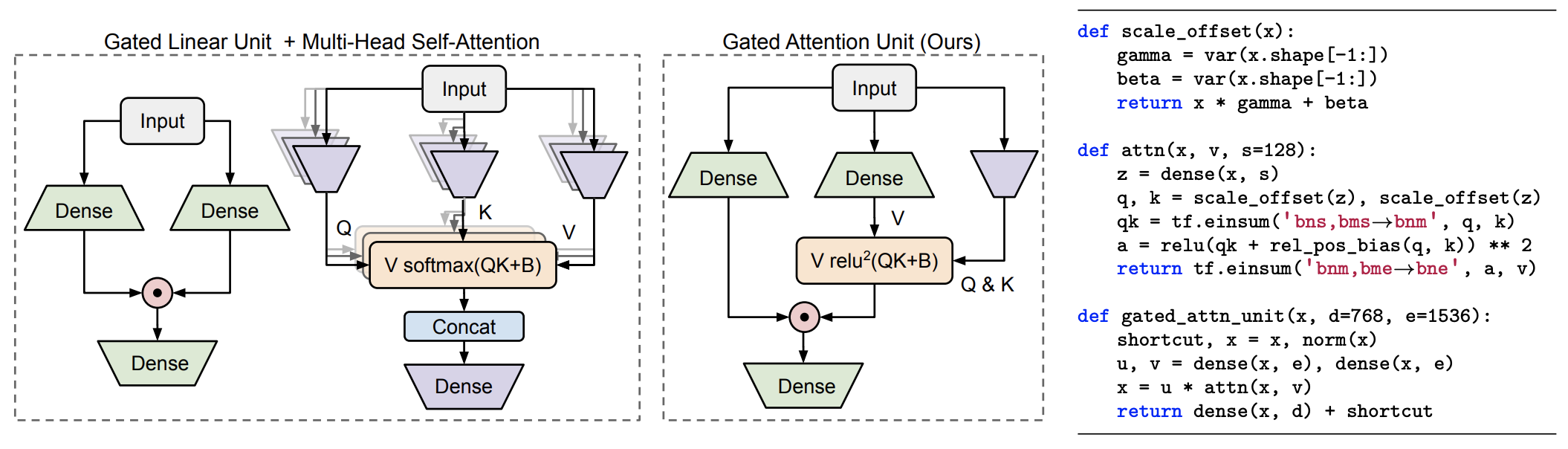
按照论文附录的参考代码,原论文化简后的缩放因子实际上是 $\frac{1}{n^2}$,苏剑林认为 $\frac{1}{ns}$ 会更加合理一些,不然当 $n$ 足够大时,每一项注意力都过小了。
特别地,由于 GLU 本身性能就很强,对 Attention 的依赖非常弱,以至于作者们发现:只用一个头就够了!标准 Transformer 用的是多头注意力机制,在运算过程中需要产生 $bhn^2$ 大小的矩阵,$b$ 是 batch_size 而 $h$ 是头数。而只用一个头的 GAU,就可以达到相同甚至更好的效果,不仅提高了计算速度,还降低了显存占用量。
当 GAU 只有一个头时,$\boldsymbol{W}_z$ 的参数量就很少了,主要参数量在 $\boldsymbol{W}_u,\boldsymbol{W}_v,\boldsymbol{W}_o$ 上,所以 GAU 的参数量大约为 $3de$;而在标准 Transformer 中,Attention的参数量为 $4d^2$,FFN的参数量为 $8d^2$(标准 FFN 中一般是 $e=4d$),所以总参数量为 $12d^2$。因此,从参数量看,当 $e=2d$ 时,两层 GAU 大致上就等于原来的 Attention+FFN。
所以,在 GAU 的实验中,作者都固定 $e=2d$,那么“$n$ 层 Attention+ $n$ 层 FFN”的标准 Transformer 模型,对应的就是“$2n$ 层 GAU”的新模型,记为 FLASH-Quad,其中 Quad 是“Quadratic”的简写,表明复杂度依然是二次的。
代码地址为:
-
Keras 版 GAU:bert4keras/layers.py#L583
-
PyTorch 版 FLASH-Quad:https://github.com/JunnYu/FLASHQuad_pytorch
GAU 长度泛化问题
当前 NLP 主流的预训练模式都是在一个固定长度(比如 512)上进行,然后直接将预训练好的模型用于不同长度的任务中,仿佛模型可以自动泛化到不同长度是一个“理所应当”的能力。但是苏剑林在做了 Base 版的 GAU 实验后才发现 GAU 的长度泛化能力并不如想象中好。
回顾 GAU 的形式:
\[\boldsymbol{A}=\frac{1}{n}\text{relu}^2\left(\frac{\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}}{\sqrt{s}}\right)=\frac{1}{ns}\text{relu}^2\left(\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}\right)\]这就有一个问题:如果预训练时尽量将样本整理成同一长度(比如 512),那么在预训练阶段 $n$ 相当于一个常数,如果将它用于其他长度(比如 64、128)微调,那么这个 $n$ 是否应该改为样本长度呢?答案很反直觉:$n$ 固定为 512 的微调效果居然比 $n$ 取样本长度的效果要明显好!GAU 的整体运算可以简写成 $\boldsymbol{O}=(\boldsymbol{U}\odot\boldsymbol{A}\boldsymbol{V})\boldsymbol{W}_o$,其中 $\boldsymbol{U},\boldsymbol{V},\boldsymbol{W}_o$ 都是 token-wise 的,不会受到长度变化的影响,所以问题只能是出现在 $\boldsymbol{A}$ 中。
GAU 的 Attention 与标准 Attention 的差异有两点:一是多头 Attention 变成单头 Attention,但这顶多会让效果有一定波动,所以问题是出现在归一化方式上,即 Attention 的 $\text{softmax}$ 换成 $\frac{1}{n}\text{relu}^2(\cdot)$ 所带来的。Softmax 的操作是:
\[a_{i,j} = \frac{1}{Z_i}\exp\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right),\quad Z_i = \sum_{i=1}^n \exp\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right)\tag{5}\]由于注意力只会“聚焦”到比较重要的几个 token 上,所以位置为 $i$ 的 Attention 基本上就聚焦在 $i$ 附近的若干 token 上,超出一定距离后就基本为 0 了,即存在某个常数 $k$,使得 $|j-i|\geq k$ 时 $\exp\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right)$ 都接近于 0,这样 $Z_i$ 应该更接近 $\mathscr{O}(k)$ 而不是 $\mathscr{O}(n)$。回看 GAU,它的激活函数换成了 $\text{relu}^2(\cdot)$,其 Attention 情况是类似的,甚至会更稀疏。因为 $\text{relu}$ 操作有直接置零的作用,不像 $\exp(\cdot)$ 总是正的,同时 GAU “标配”的旋转位置编码 RoPE 本身自带一定的远程衰减能力。因此,GAU 的归一化因子也应该是低于 $\mathscr{O}(n)$ 的阶甚至是常数级别的。
因此,可以总结出 GAU 的三个解决方案:一是预训练和微调都用同一个固定的 $n$;二是预训练时需要用不同长度的样本来混合训练;三就是像 Softmax 那样补充上一个归一化因子,让模型自己去学:
\[a_{i,j} = \frac{1}{Z_i}\text{relu}^2\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right),\quad Z_i = \sum_{i=1}^n \text{relu}^2\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right)\tag{6}\]但是,方案一让人感觉不够自适应,方案二必须用多种长度训练显得不够优雅,方案三补充了归一化因子后形式上相比 Softmax 反而显得“臃肿”了。再加上 GAU 原论文的消融实验显示,把 $\text{relu}^2(\cdot)$ 换成 Softmax,效果基本是一致的。因此,苏剑林认为还是用 Softmax 显得更为优雅有效。
此外,泛化能力可以简单分为“内插”和“外推”两种,内插(外推)指的是测试长度小于(大于)训练长度。前面说归一化因子是常数量级,更多是在内插范围内说的。对于外推来说,如果长度足够长,$\boldsymbol{q}_i,\boldsymbol{k}_j$ 都“挤”在一起,很难保持距离超过某个范围就很接近于 0 的特性。
幸运的是,如果用 Softmax 的话,苏剑林推导出了一个“熵不变性”的版本来增强模型的外推能力:
\[Attention(Q,K,V) = softmax\left(\frac{\log_{512} n}{\sqrt{d}}QK^{\top}\right)V\tag{7}\]而 $\text{relu}^2(\cdot)$ 却无法推导出一个“熵不变性”的版本。
GAU-α
很多人在尝试 GAU 后却发现还不如标准 Transformer,比如收敛更慢、效果更差等。因此,苏剑林最近又分享了自己的训练经验,并且放出了一个尝鲜版“GAU-α”供大家测试。
GAU-α 在 CLUE 任务上的成绩单:
\[\small{\begin{array}{c|ccccccccccc} \hline & \text{iflytek} & \text{tnews} & \text{afqmc} & \text{cmnli} & \text{ocnli} & \text{wsc} & \text{csl} & \text{cmrc2018} & \text{c3} & \text{chid} & \text{cluener}\\ \hline \text{BERT} & 60.06 & 56.80 & 72.41 & 79.56 & 73.93 & 78.62 & 83.93 & 56.17 & 60.54 & 85.69 & 79.45 \\ \text{RoBERTa} & 60.64 & \textbf{58.06} & 74.05 & 81.24 & 76.00 & \textbf{87.50} & 84.50 & 56.54 & 67.66 & 86.71 & 79.47\\ \text{RoFormer} & 60.91 & 57.54 & 73.52 & 80.92 & \textbf{76.07} & 86.84 & 84.63 & 56.26 & 67.24 & 86.57 & 79.72\\ \text{RoFormerV2}^* & 60.87 & 56.54 & 72.75 & 80.34 & 75.36 & 80.92 & 84.67 & 57.91 & 64.62 & 85.09 & \textbf{81.08}\\ \hline \text{GAU-}\alpha & \textbf{61.41} & 57.76 & \textbf{74.17} & \textbf{81.82} & 75.86 & 79.93 & \textbf{85.67} & \textbf{58.09} & \textbf{68.24} & \textbf{87.91} & 80.01\\ \hline \end{array}}\]所有模型都是 Base 版,RoFormerV2*并非《RoFormerV2:自然语言理解的极限探索》中的多任务版本,而是仅仅进行了 MLM 预训练(该版本没开源),因为 GAU-α 也仅仅进行了 MLM 预训练。
模型架构: GAU-α 就是将 RoFormerV2 的 Attention+FFN 换成了两层 GAU,RoFormerV2 的特点是保留了Post Norm 结构,去掉了所有的 Bias 项,并且 Layer Norm 换成了 RMS Norm 的最简单变体,在 GAU-α 中也是如此。
归一化: GAU-α 的 Attention 归一化选取了前面提到的具有较好外推能力的熵不变性 Softmax。
训练方式: 在初始化方面,按照《训练1000层的Transformer究竟有什么困难?》进行了调整,因此无须 Wamrup 就可以直接训练,优化器用的是 LAMB,学习率分段线性衰减;预训练任务用的是全词 MLM,分词工具用百度的 LAC,这些跟 RoFormerV2 都是对齐的。
代码地址为:
参考
[1] FLASH:可能是近来最有意思的高效Transformer设计
[2] 听说Attention与Softmax更配哦~
[3] GAU-α:尝鲜体验快好省的下一代Attention