在之前的教程中,我们介绍了 Keras 网络的模型与网络层,并且通过许多示例展示了网络的搭建方式。大家都注意到了,在构建网络的过程中,损失函数、优化器、激活函数等都是需要自定义的网络配置项,下面我们对这些网络配置进行详细的介绍。
损失函数
目标函数 objectives
目标函数,或称损失函数,是编译一个模型必须的两个参数之一:
model.compile(loss='mean_squared_error', optimizer='sgd')
可以通过传递预定义目标函数名字指定目标函数,也可以传递一个 Theano/TensroFlow 的符号函数作为目标函数,该函数对每个数据点应该只返回一个标量值,并以下列两个参数为参数:
- y_true:真实的数据标签,Theano/TensorFlow 张量
- y_pred:预测值,与 y_true 相同 shape 的 Theano/TensorFlow 张量
from keras import losses
model.compile(loss=losses.mean_squared_error, optimizer='sgd')
真实的优化目标函数是在各个数据点得到的损失函数值之和的均值。
预定义目标函数
- mean_squared_error 或 mse:均方误差
- mean_absolute_error 或 mae:平均绝对误差
- mean_absolute_percentage_error 或 mape:平均绝对百分比误差
- mean_squared_logarithmic_error 或 msle:均方误差对数
- squared_hinge
- hinge
- binary_crossentropy:对数损失,logloss
- logcosh
- categorical_crossentropy:亦称作多类的对数损失,注意使用该目标函数时,需要将标签转化为形如
(nb_samples, nb_classes)的二值序列 - sparse_categorical_crossentrop:如上,但接受稀疏标签。注意,使用该函数时仍然需要你的标签与输出值的维度相同,你可能需要在标签数据上增加一个维度:
np.expand_dims(y,-1) - kullback_leibler_divergence:从预测值概率分布 Q 到真值概率分布 P 的信息增益,用以度量两个分布的差异
- poisson:即
(predictions - targets * log(predictions))的均值 - cosine_proximity:即预测值与真实标签的余弦距离平均值的相反数
注意: 当使用”categorical_crossentropy”作为目标函数时,标签应该为多类模式,即 one-hot 编码的向量,而不是单个数值.。可以使用工具中的 to_categorical 函数完成该转换,示例如下:
from keras.utils.np_utils import to_categorical
categorical_labels = to_categorical(int_labels, num_classes=None)
优化器
优化器是编译 Keras 模型必要的两个参数之一。
from keras import optimizers
model = Sequential()
model.add(Dense(64, init='uniform', input_shape=(10,)))
model.add(Activation('tanh'))
model.add(Activation('softmax'))
sgd = optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(loss='mean_squared_error', optimizer=sgd)
可以在调用 model.compile() 之前初始化一个优化器对象,然后传入该函数(如上所示),也可以在调用 model.compile() 时传递一个预定义优化器名。在后者情形下,优化器的参数将使用默认值。
# 传递一个预定义优化器名
model.compile(loss='mean_squared_error', optimizer='sgd')
所有优化器都可用的参数
参数 clipnorm 和 clipvalue 是所有优化器都可以使用的参数,用于对梯度进行裁剪。示例如下:
from keras import optimizers
# 所有参数的梯度会被剪裁到最大范数为1.
sgd = optimizers.SGD(lr=0.01, clipnorm=1.)
from keras import optimizers
# 所有参数梯度会被剪裁到最大值为0.5,最小值为-0.5
sgd = optimizers.SGD(lr=0.01, clipvalue=0.5)
SGD
随机梯度下降法,支持动量参数,支持学习衰减率,支持 Nesterov 动量。
keras.optimizers.SGD(lr=0.01, momentum=0.0, decay=0.0, nesterov=False)
- lr:大于 0 的浮点数,学习率
- momentum:大于 0 的浮点数,动量参数
- decay:大于 0 的浮点数,每次更新后的学习率衰减值
- nesterov:布尔值,确定是否使用 Nesterov 动量
RMSprop
除学习率可调整外,建议保持优化器的其他默认参数不变。该优化器通常是面对递归神经网络时的一个良好选择。
keras.optimizers.RMSprop(lr=0.001, rho=0.9, epsilon=1e-06)
- lr:大于 0 的浮点数,学习率
- rho:大于 0 的浮点数
- epsilon:大于 0 的小浮点数,防止除 0 错误
Adam
该优化器的默认值来源于参考文献。
keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-08)
- lr:大于 0 的浮点数,学习率
- beta_1:浮点数, 0<beta<1,通常很接近 1
- beta_2:浮点数, 0<beta<1,通常很接近 1
- epsilon:大于 0的小浮点数,防止除 0 错误
激活函数
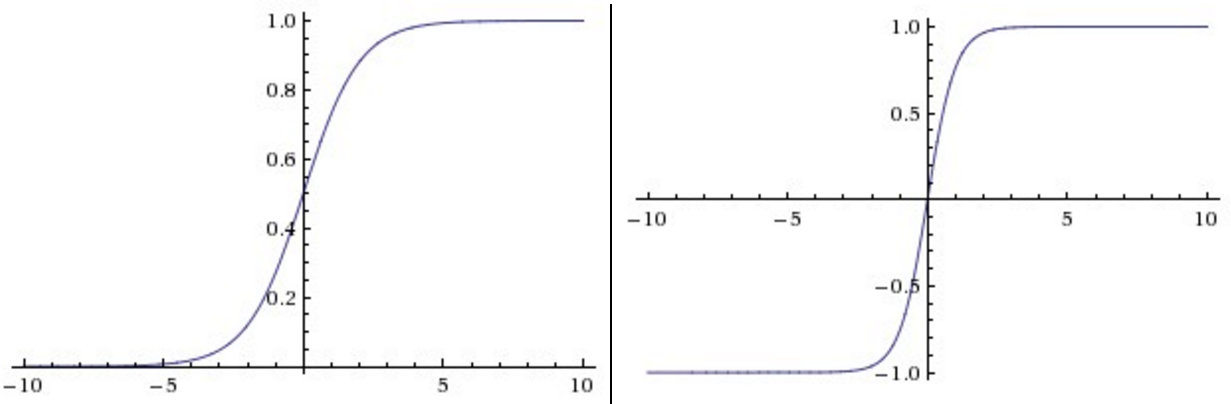
激活函数用于在模型中引入非线性。激活函数 $\text{sigmoid}$ 与 $\tanh$ 曾经很流行,但现在很少用于视觉模型了,主要原因在于当输入的绝对值较大时,其导数接近于零,梯度的反向传播过程将被中断,出现梯度消散的现象。
$\text{ReLU}$ 是一个很好的替代:
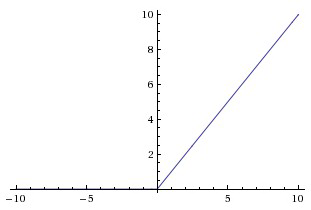
相比于 $\text{sigmoid}$ 与 $\tanh$,它有两个优势:
- 没有饱和问题,大大缓解了梯度消散的现象,加快了收敛速度。
- 实现起来非常简单,加速了计算过程。
$\text{ReLU}$ 有一个缺陷,就是它可能会永远“死”掉:
假如有一组二维数据 $X$ $(x_1, x_2)$ 分布在 $x_1:[0,1], x_2:[0,1]$ 的区域内,有一组参数 $W$ $(w_1, w_2)$ 对 $X$ 做线性变换,并将结果输入到 $\text{ReLU}$。 \(F = w_1*x_1 + w_2*x_2\) 如果 $w_1 = w_2 = -1$,那么无论 $X$ 如何取值,$F$ 必然小于等于零。那么 $\text{ReLU}$ 函数对 $F$ 的导数将永远为零。这个 $\text{ReLU}$ 节点将永远不参与整个模型的学习过程。
造成上述现象的原因是 $\text{ReLU}$ 在负区间的导数为零,为了解决这一问题,人们发明了 $\text{Leaky ReLU}$、 $\text{Parametric ReLU}$、 $\text{Randomized ReLU}$ 等变体。他们的中心思想都是为 $\text{ReLU}$ 函数在负区间赋予一定的斜率,从而让其导数不为零(这里设斜率为 $\alpha$)。
$\text{Leaky ReLU}$ 就是直接给 $\alpha$ 指定一个值,整个模型都用这个斜率:
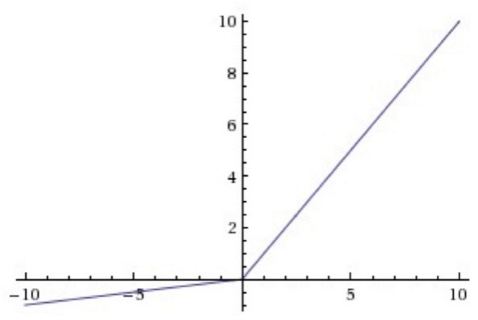
$\text{Parametric ReLU}$ 将 $\alpha$ 作为一个参数,通过学习获取它的最优值。$\text{Randomized ReLU}$ 为 $\alpha$ 规定一个区间,然后在区间内随机选取 $\alpha$ 的值。
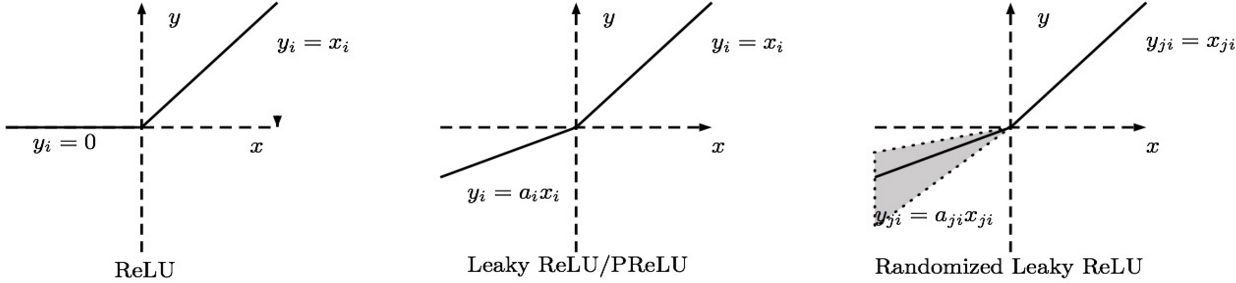
在实践中,$\text{Parametric ReLU}$ 和 $\text{Randomized ReLU}$ 都是可取的。
激活函数可以通过设置单独的激活层实现,也可以在构造层对象时通过传递 activation 参数实现。
from keras.layers import Activation, Dense
model.add(Dense(64))
model.add(Activation('tanh'))
等价于:
model.add(Dense(64, activation='tanh'))
也可以通过传递一个逐元素运算的 Theano/TensorFlow 函数来作为激活函数:
from keras import backend as K
def tanh(x):
return K.tanh(x)
model.add(Dense(64, activation=tanh))
model.add(Activation(tanh)
预定义激活函数
- softmax:对输入数据的最后一维进行 softmax,输入数据应形如
(nb_samples, nb_timesteps, nb_dims)或(nb_samples, nb_dims) - elu
- softplus
- softsign
- relu
- tanh
- sigmoid
- hard_sigmoid
- linear
高级激活函数
对于简单的 Theano/TensorFlow 不能表达的复杂激活函数,如含有可学习参数的激活函数,可通过高级激活函数实现,如 PReLU,LeakyReLU 等。下面我们详细介绍一下高级激活层。
高级激活层
LeakyReLU 层
LeakyRelU 是修正线性单元(Rectified Linear Unit,ReLU)的特殊版本,当不激活时,LeakyReLU 仍然会有非零输出值,从而获得一个小梯度,避免 ReLU 可能出现的神经元“死亡”现象。
keras.layers.advanced_activations.LeakyReLU(alpha=0.3)
- alpha:大于 0 的浮点数,代表激活函数图像中第三象限线段的斜率
该层输入 shape 任意,当使用该层为模型首层时需指定 input_shape 参数,输出 shape 与输入相同。
PReLU 层
该层为参数化的 ReLU(Parametric ReLU),表达式是:$f(x)=\begin{cases}\alpha*x&, x\lt0\\x&,x\ge0\end{cases}$,此处的 $\alpha$ 为一个与 xshape 相同的可学习的参数向量。
keras.layers.advanced_activations.PReLU(shared_axes=None)
- shared_axes:该参数指定的轴将共享同一组科学系参数,例如假如输入特征图是从 2D 卷积过来的,具有形如
(batch, height, width, channels)这样的 shape,则或许你会希望在空域共享参数,这样每个 filter 就只有一组参数,设定shared_axes=[1,2]可完成该目标
ELU 层
ELU 层是指数线性单元(Exponential Linera Unit),表达式为: 该层为参数化的 ReLU(Parametric ReLU),表达式是:$f(x)=\begin{cases}\alpha*(\exp(x)-1)&, x\lt0\\x&,x\ge0\end{cases}$。
keras.layers.advanced_activations.ELU(alpha=1.0)
- alpha:控制负因子的参数
该层输入 shape 任意,当使用该层为模型首层时需指定 input_shape 参数,输出 shape 与输入相同。
ThresholdedReLU 层
该层是带有门限的 ReLU,表达式是:$f(x)=\begin{cases}x&, x\gt\theta\\0&,\text{otherwise}\end{cases}$。
keras.layers.advanced_activations.ThresholdedReLU(theta=1.0)
- theata:大或等于 0 的浮点数,激活门限位置
该层输入 shape 任意,当使用该层为模型首层时需指定 input_shape 参数,输出 shape 与输入相同。
数据预处理
填充序列
将长为 nb_samples 的序列(标量序列)转化为形如 (nb_samples,nb_timesteps) 的 2D numpy array。如果提供了参数 maxlen,nb_timesteps=maxlen,否则其值为最长序列的长度。其他短于该长度的序列都会在后部填充 0以达到该长度。长于 nb_timesteps 的序列将会被截断,以使其匹配目标长度。padding 和截断发生的位置分别取决于 padding 和 truncating。
keras.preprocessing.sequence.pad_sequences(sequences, maxlen=None, dtype='int32',
padding='pre', truncating='pre', value=0.)
- sequences:浮点数或整数构成的两层嵌套列表
- maxlen:None 或整数,为序列的最大长度。大于此长度的序列将被截短,小于此长度的序列将在后部填 0
- dtype:返回的 numpy array 的数据类型
- padding:“pre”或“post”,确定当需要补 0 时,在序列的起始还是结尾补
- truncating:“pre”或“post”,确定当需要截断序列时,从起始还是结尾截断
- value:浮点数,此值将在填充时代替默认的填充值 0
返回值返回形如 (nb_samples,nb_timesteps) 的 2D 张量。
句子分割
本函数将一个句子拆分成单词构成的列表。
keras.preprocessing.text.text_to_word_sequence(text, filters=base_filter(), lower=True, split=" ")
- text:字符串,待处理的文本
- filters:需要滤除的字符的列表或连接形成的字符串,例如标点符号。默认值为
base_filter(),包含标点符号,制表符和换行符等 - lower:布尔值,是否将序列设为小写形式
- split:字符串,单词的分隔符,如空格
返回值为字符串列表。
one-hot 编码
本函数将一段文本编码为 one-hot 形式的码,即仅记录词在词典中的下标。
从定义上,当字典长为 n 时,每个单词应形成一个长为 n 的向量,其中仅有单词本身在字典中下标的位置为 1,其余均为 0,这称为 one-hot。
为了方便起见,函数在这里仅把“1”的位置,即字典中词的下标记录下来。
keras.preprocessing.text.one_hot(text, n, filters=base_filter(), lower=True, split=" ")
- text:字符串,待处理的文本
- n:整数,字典长度
- filters:需要滤除的字符的列表或连接形成的字符串,例如标点符号。默认值为
base_filter(),包含标点符号,制表符和换行符等 - lower:布尔值,是否将序列设为小写形式
- split:字符串,单词的分隔符,如空格
返回值为整数列表,每个整数是 $[1,n]$ 之间的值,代表一个单词(不保证唯一性,即如果词典长度不够,不同的单词可能会被编为同一个码)。
分词器
Tokenizer 是一个用于向量化文本,或将文本转换为序列(即单词在字典中的下标构成的列表,从 1 算起)的类。
keras.preprocessing.text.Tokenizer(nb_words=None, filters=base_filter(), lower=True, split=" ")
- nb_words:None 或整数,处理的最大单词数量。若被设置为整数,则分词器将被限制为处理数据集中最常见的
nb_words-1个单词 - filters:需要滤除的字符的列表或连接形成的字符串,例如标点符号。默认值为
base_filter(),包含标点符号,制表符和换行符等 - lower:布尔值,是否将序列设为小写形式
- split:字符串,单词的分隔符,如空格
类方法:
- fit_on_texts(texts)
- texts:要用以训练的文本列表
- texts_to_sequences(texts)
- texts:待转为序列的文本列表
- 返回值:序列的列表,列表中每个序列对应于一段输入文本
- texts_to_sequences_generator(texts)
- 本函数是
texts_to_sequences的生成器函数版 - texts:待转为序列的文本列表
- 返回值:每次调用返回对应于一段输入文本的序列
- 本函数是
- texts_to_matrix(texts, mode):
- texts:待向量化的文本列表
- mode:“binary”、“count”、“tfidf”、“freq”之一,默认为“binary”
- 返回值:形如
(len(texts), nb_words)的 numpy array
- fit_on_sequences(sequences):
- sequences:要用以训练的序列列表
- sequences_to_matrix(sequences):
- sequences:待向量化的序列列表
- mode:“binary”、“count”、“tfidf”、“freq”之一,默认为“binary”
- 返回值:形如
(len(sequences), nb_words)的 numpy array
属性:
- word_counts:字典,将单词(字符串)映射为它们在训练期间出现的次数。仅在调用
fit_on_texts之后设置。 - word_docs:字典,将单词(字符串)映射为它们在训练期间所出现的文档或文本的数量。仅在调用
fit_on_texts之后设置。 - word_index:字典,将单词(字符串)映射为它们的排名或者索引。仅在调用
fit_on_texts之后设置。 - document_count:整数。分词器被训练的文档(文本或者序列)数量。仅在调用
fit_on_texts或fit_on_sequences之后设置。
本文整理自《Keras中文文档》