本文将进一步介绍神经网络的核心组件,即层、网络、目标函数和优化器。并且通过三个介绍性示例深入讲解如何使用神经网络解决实际问题,这三个示例分别是:
- 将电影评论划分为正面或负面(二分类问题)
- 将新闻按主题分类(多分类问题)
- 根据房地产数据估算房屋价格(回归问题)
神经网络剖析
训练神经网络主要围绕以下四个方面:
- 层,多个层组合成网络(或模型)。
- 输入数据和相应的目标。
- 损失函数,即用于学习的反馈信号。
- 优化器,决定学习过程如何进行。
你可以将这四者的关系可视化,如下图所示:多个层链接在一起组成了网络,将输入数据映射为预测值。然后损失函数将这些预测值与目标进行比较,得到损失值,用于衡量网络预测值与预期结果的匹配程度。优化器使用这个损失值来更新网络的权重。

层:深度学习的基础组件
神经网络的基本数据结构是层,层将一个或多个输入张量转换为一个或多个输出张量。大多数的层是有权重的,权重是利用随机梯度下降学到的一个或多个张量,其中包含网络的知识。
不同的张量格式与不同的数据处理类型需要用到不同的层。例如:
- 简单的向量数据保存在形状为
(samples, features)的 2D 张量中,通常用全连接层 (fully connected layer,对应于 Keras 的Dense类) 来处理。 - 序列数据保存在形状为
(samples, timesteps, features)的 3D 张量中,通常用循环层 (recurrent layer,比如 Keras 的LSTM层) 来处理。 - 图像数据保存在 4D 张量中,通常用二维卷积层(Keras 的
Conv2D)来处理。
在 Keras 中,构建深度学习模型就是将相互兼容的多个层拼接在一起。层兼容性 (layer compatibility) 指的是每一层只接受特定形状的输入张量,并返回特定形状的输出张量。例如:
from keras import layers
layer = layers.Dense(32, input_shape=(784,)) ←有32个输出单元的密集层
这个层只接受维度大小为 784 的 2D 张量( input_shape 中不包含数据的 batch 大小)作为输入,并且返回一个大小为 32 的张量。因此,这个层后面只能连接一个接受 32 维向量作为输入的层。
Keras 中除了第一层以外,向模型中添加的层都会自动匹配输入层的形状,例如:
from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(32, input_shape=(784,)))
model.add(layers.Dense(32))
其中第二层没有输入形状(input_shape)的参数,它可以自动推导出输入形状等于上一层的输出形状。
模型:层构成的网络
深度学习模型是层构成的有向无环图。最常见就是层的线性堆叠,将单一输入映射为单一输出。常见的网络拓扑结构如下。
- 双分支 (two-branch) 网络
- 多头 (multihead) 网络
- Inception 模块
网络的拓扑结构定义了一个假设空间 (hypothesis space)。回顾《Keras深度学习笔记(一):什么是深度学习》里机器学习的定义:“在预先定义好的假设空间中,利用反馈信号的指引来寻找输入数据的有用表示。”选定了网络拓扑结构,意味着将假设空间限定为一系列特定的张量运算,然后为这些张量运算的权重张量找到一组合适的值。
选择正确的网络架构更像是一门艺术而不是科学。合格的神经网络架构师会明白对于特定问题哪些架构有用、哪些架构无用。
损失函数与优化器:配置学习过程的关键
一旦确定了网络架构,还需要选择以下两个参数。
- 损失函数(目标函数)——在训练过程中需要将其最小化。它能够衡量当前任务是否已成功完成。
- 优化器——决定如何基于损失函数对网络进行更新。它执行的是随机梯度下降(SGD)的某个变体。
具有多个输出的神经网络可能具有多个损失函数(每个输出对应一个损失函数)。但是梯度下降过程必须基于单个标量损失值,通常将所有损失函数取平均,变为一个标量值。
网络的目的是使损失尽可能最小化,因此选择正确的目标函数对解决问题是非常重要的。
幸运的是,对于分类、回归、序列预测等常见问题,可以遵循一些简单的指导原则。例如:
- 对于二分类问题,可以使用二元交叉熵 (binary crossentropy) 损失函数;
- 对于多分类问题,可以用分类交叉熵 (categorical crossentropy) 损失函数;
- 对于回归问题,可以用均方误差 (mean-squared error) 损失函数;
- 对于序列学习问题,可以用联结主义时序分类 (CTC,connectionist temporal classification) 损失函数。
只有在面对真正全新的研究问题时,我们才需要自主开发目标函数。
Keras 简介
典型的 Keras 工作流程为:
- 定义训练数据:输入张量和目标张量。
- 定义层组成的网络(模型),将输入映射到目标。
- 配置学习过程:选择损失函数、优化器和需要监控的指标。
- 调用模型的
fit方法在训练数据上进行迭代。
定义模型有两种方法:一种是使用 Sequential 类(仅用于层的线性堆叠,这是最常见的网络架构),另一种是函数式 API (functional API),用于层组成的有向无环图,可以构建任意形式的架构。
例如利用 Sequential 类定义的两层模型:
from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(32, activation='relu', input_shape=(784,)))
model.add(layers.Dense(10, activation='softmax'))
下面是用函数式 API 定义的相同模型:
input_tensor = layers.Input(shape=(784,))
x = layers.Dense(32, activation='relu')(input_tensor)
output_tensor = layers.Dense(10, activation='softmax')(x)
model = models.Model(inputs=input_tensor, outputs=output_tensor)
利用函数式 API 可以操纵模型处理的数据张量,并将层应用于这个张量,就好像这些层是函数一样。
接下来是配置学习过程,就是在编译这一步指定模型使用的优化器和损失函数,以及训练过程中想要监控的指标。下面是单一损失函数的例子:
from keras import optimizers
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss='mse',
metrics=['accuracy'])
最后,学习过程就是通过 fit() 方法将输入数据的 Numpy 数组(和对应的目标数据)传入模型:
model.fit(input_tensor, target_tensor, batch_size=128, epochs=10)
为了培养可靠的直觉:哪种类型的网络架构适合解决哪种类型的问题?如何选择正确的学习配置?如何调节模型使其给出你想要的结果?下面我们讲解三个基本示例,分别是二分类问题、多分类问题和回归问题。
电影评论分类:二分类问题
二分类问题可能是应用最广泛的机器学习问题。下面我们将根据电影评论的文字内容将其划分为正面或负面。
IMDB 数据集
IMDB 数据集包含来自互联网电影数据库 (IMDB) 的 50,000 条严重两极分化的评论。数据集被分为用于训练的 25,000 条评论与用于测试的 25,000 条评论,训练集和测试集都包含 50% 的正面评论和 50% 的负面评论。
为什么要将训练集和测试集分开?
模型在训练数据上的表现很好,并不意味着它在前所未见的数据上也会表现得很好,我们真正关心的是模型在新数据上的性能。
IMDB 数据集也内置于 Keras 库,并且已经过预处理:评论(单词序列)已经被转换为整数序列,其中每个整数代表字典中的某个单词。(第一次运行时会下载大约 80MB 的数据)
from keras.datasets import imdb
# 加载 IMDB 数据集
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
参数 num_words=10000 的意思是仅保留训练数据中前 10,000 个最常出现的单词。低频单词将被舍弃。这样得到的向量数据不会太大,便于处理。
train_data 和 test_data 这两个变量都是评论组成的列表,每条评论又是单词索引组成的列表(表示一系列单词)。train_labels 和 test_labels 都是 0 和 1 组成的列表,其中 0 代表负面 (negative),1 代表正面 (positive)。
>>> train_data[0]
[1, 14, 22, 16, ... 178, 32]
>>> train_labels[0]
1
由于限定为前 10,000 个最常见的单词,单词索引都不会超过 10,000。
>>> max([max(sequence) for sequence in train_data])
9999
可以将某条评论解码为英文单词:
word_index = imdb.get_word_index() # word_index是一个将单词映射为整数索引的字典
# 键值颠倒,将整数索引映射为单词
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
# 将评论解码
decoded_review = ' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[0]])
注意,索引减去了 3,因为 0、1、2 是分别为 padding (填充)、start of sequence (序列开始)、unknown (未知词) 保留的索引。
准备数据
你不能将整数序列直接输入神经网络。你需要将列表转换为张量。转换方法有以下两种。
- 填充列表,使其具有相同的长度,再将列表转换成形状为
(samples, word_indices)的整数张量,然后网络第一层使用能处理这种整数张量的层(即Embedding层,本书后面会详细介绍)。 - 对列表进行 one-hot 编码,将其转换为 0 和 1 组成的向量。举个例子,序列
[3, 5]将会被转换为 10,000 维向量,只有索引为 3 和 5 的元素是 1,其余元素都是 0。然后网络第一层可以用Dense层,它能够处理浮点数向量数据。
下面我们采用后一种方法将数据向量化。为了加深理解,可以手动实现这一方法:
import numpy as np
def vectorize_sequences(sequences, dimension=10000):
# 创建一个形状为(len(sequences), dimension)的零矩阵
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1. # 将results[i]的指定索引设为1
return results
x_train = vectorize_sequences(train_data) ←将训练数据向量化
x_test = vectorize_sequences(test_data) ←将测试数据向量化
样本现在变成了这样:
>>> x_train[0]
array([ 0., 1., 1., ..., 0., 0., 0.])
我们还应该将标签向量化,这很简单。
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')
现在可以将数据输入到神经网络中。
构建网络
输入数据是向量,而标签是标量(1 和 0),这是会遇到的最简单的情况。有一类网络在这种问题上表现很好,就是带有 relu 激活的全连接层(Dense)的简单堆叠,比如 Dense(16, activation='relu')。
传入 Dense 层的参数 16 是该层隐藏单元的个数。一个隐藏单元 (hidden unit) 是该层表示空间的一个维度。前面讲过,每个带有 relu 激活的 Dense 层都实现了下列张量运算:
16 个隐藏单元对应的权重矩阵 $W$ 的形状为 (input_dimension, 16),与 $W$ 做点积相当于将输入数据投影到 16 维表示空间中(然后再加上偏置向量 $b$ 并应用 $\text{relu}$ 运算)。隐藏单元越多(即更高维的表示空间),网络越能够学到更加复杂的表示,但网络的计算代价也变得更大,而且可能会导致过拟合。
对于这种 Dense 层的堆叠,我们需要确定以下两个关键架构:
- 网络有多少层;
- 每层有多少个隐藏单元。
这里我们选择:
- 两个中间层,每层都有 16 个隐藏单元;
- 第三层输出一个标量,预测当前评论的情感。
from keras import models
from keras import layers
# 模型定义
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
网络的结构如下图所示:
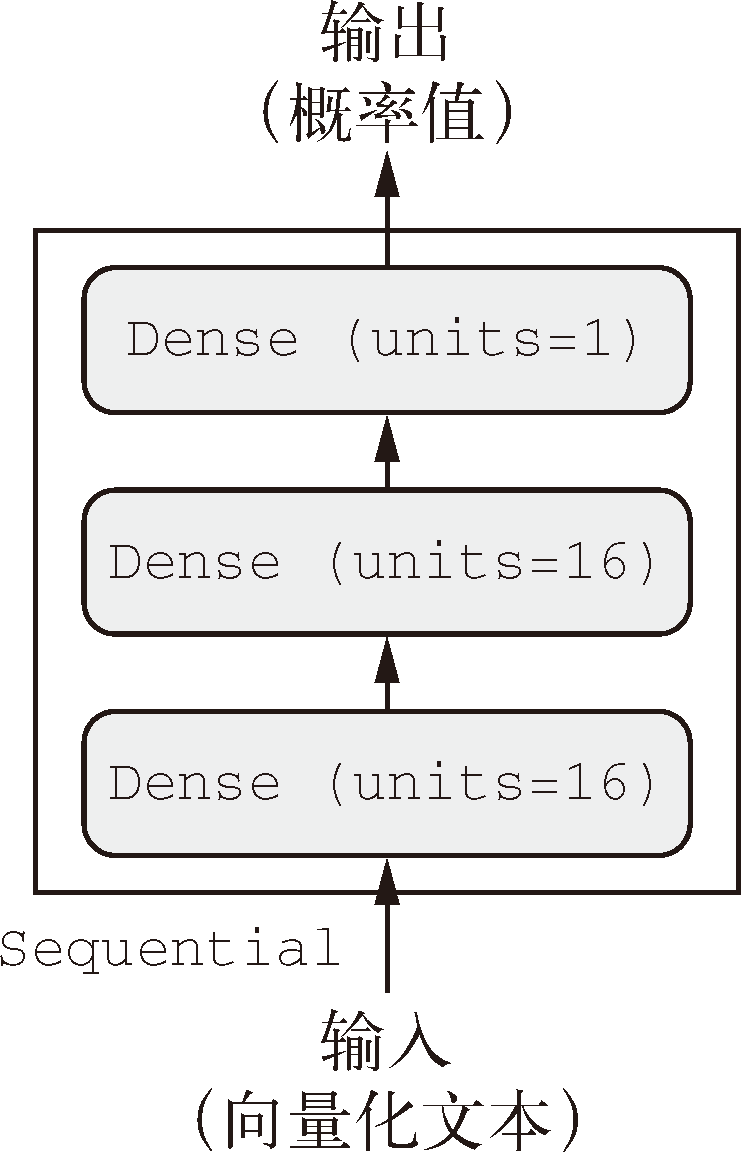
中间层使用 $\text{relu}$ 作为激活函数,最后一层使用 $\text{sigmoid}$ 激活以输出一个 $0\sim1$ 范围内的概率值(表示样本的目标值等于 1 的可能性,即评论为正面的可能性)。
$\text{relu}$ (rectified linear unit,整流线性单元) 函数将所有负值归零,而 $\text{sigmoid}$ 函数则将任意值“压缩”到 $[0, 1]$ 区间内,其输出值可以看作概率值。
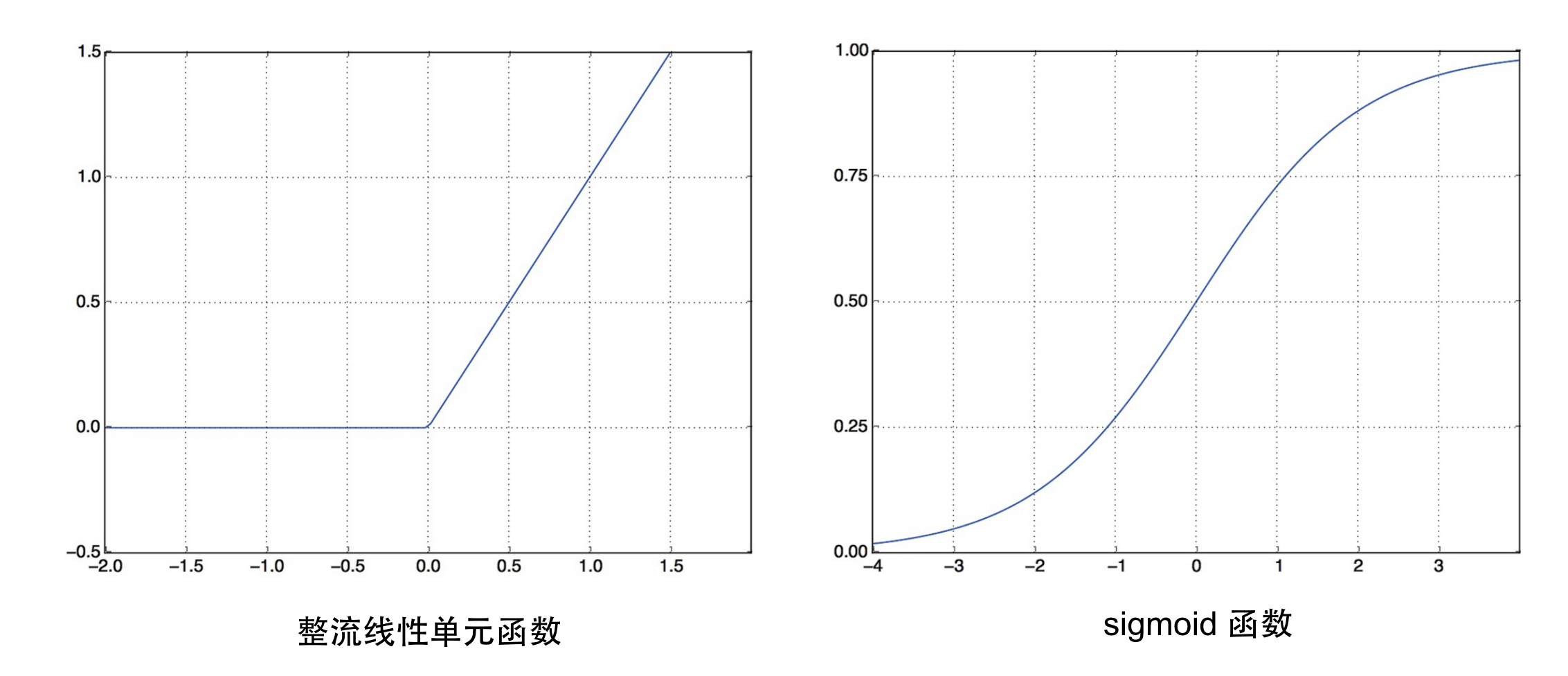
激活函数
如果没有 $\text{relu}$ 等非线性激活函数,
\[output = \text{dot}(W, input) + b\]Dense层将只包含两个线性运算——点积和加法:这样
Dense层就只能学习输入数据的线性变换(仿射变换),这种假设空间非常有限,因为多个线性层堆叠实现的仍是线性运算,添加层数并不会扩展假设空间。为了得到更丰富的假设空间,从而充分利用多层表示的优势,我们需要添加非线性或激活函数。$\text{relu}$ 是深度学习中最常用的激活函数,还有许多其他函数,比如 $\text{prelu}$、$\text{elu}$ 等。
最后,我们需要选择损失函数和优化器。由于是一个二分类问题,网络输出是一个概率值(网络最后一层使用 $\text{sigmoid}$ 激活函数,仅包含一个单元),那么最好使用 binary_crossentropy (二元交叉熵) 损失,当然也可以使用 mean_squared_error(均方误差)。但对于输出概率值的模型,交叉熵 (crossentropy) 往往是最好的选择。交叉熵是来自于信息论领域的概念,用于衡量概率分布之间的距离,在这个例子中就是真实分布与预测值之间的距离。
这里我们用 rmsprop 优化器和 binary_crossentropy:
# 编译模型
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
rmsprop、binary_crossentropy 和 accuracy 都是 Keras 内置的一部分。如果需要自定义优化器的参数,可通过向 optimizer 参数传入一个优化器类实例来实现;或者需要自定义的损失函数或指标函数,可通过向 loss 和 metrics 参数传入函数对象来实现:
from keras import optimizers
# 配置优化器
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss='binary_crossentropy',
metrics=['accuracy'])
from keras import losses
from keras import metrics
# 使用自定义的损失和指标
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss=losses.binary_crossentropy,
metrics=[metrics.binary_accuracy])
验证模型
为了在训练过程中监控模型在前所未见的数据上的精度,我们需要将原始训练数据留出 10,000 个样本作为验证集。
x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]
现在使用 512 个样本组成的小批量,将模型训练 20 个轮次。与此同时,我们还监控在留出的 10,000 个样本上的损失和精度,通过将验证数据传入 validation_data 参数来完成。
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
# 训练模型
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))
注意,调用 model.fit() 返回了一个 History 对象。这个对象有一个成员 history,它是一个字典,包含训练过程中的所有数据:
>>> history_dict = history.history
>>> history_dict.keys()
dict_keys(['val_acc', 'acc', 'val_loss', 'loss'])
字典中包含 4 个条目,对应训练过程和验证过程中监控的指标。下面我们使用 Matplotlib 在同一张图上绘制训练损失和验证损失,以及训练精度和验证精度。
import matplotlib.pyplot as plt
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
# 绘制训练损失和验证损失
plt.plot(epochs, loss_values, 'bo', label='Training loss') #'bo'表示蓝色圆点
plt.plot(epochs, val_loss_values, 'b', label='Validation loss') #'b'表示蓝色实线
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
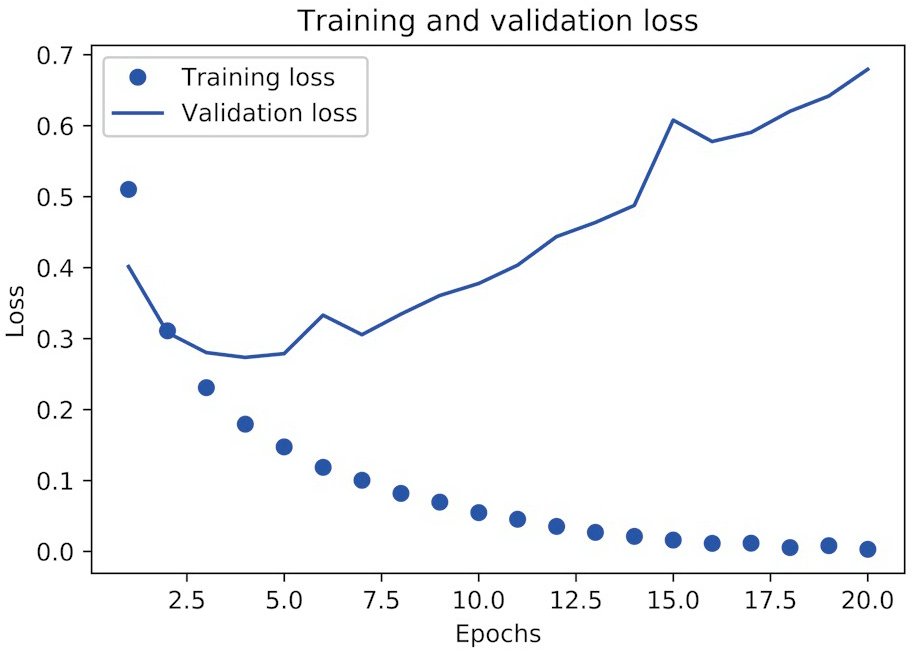
plt.clf() # 清空图像
acc = history_dict['acc']
val_acc = history_dict['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
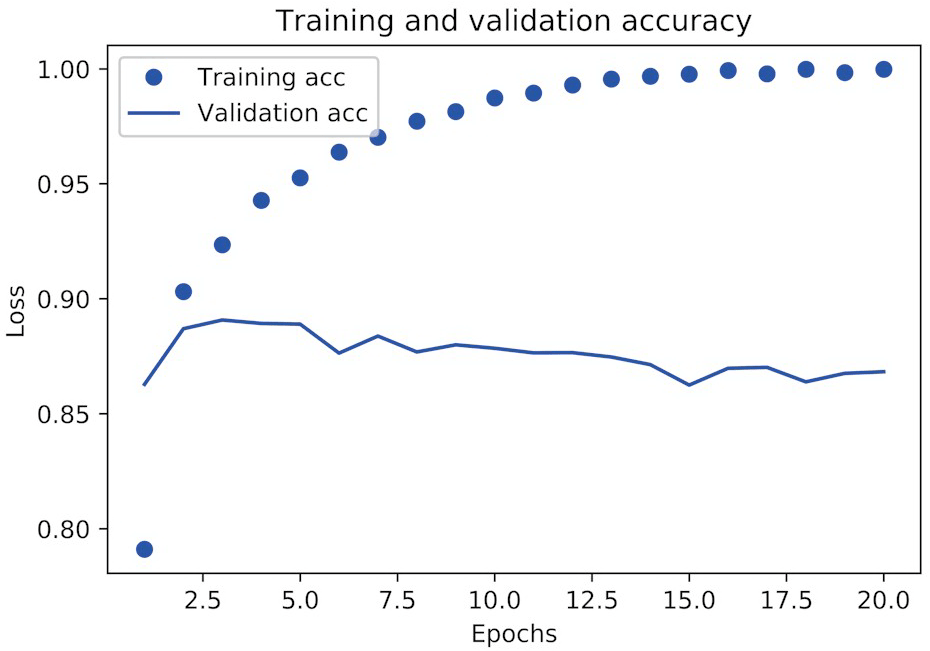
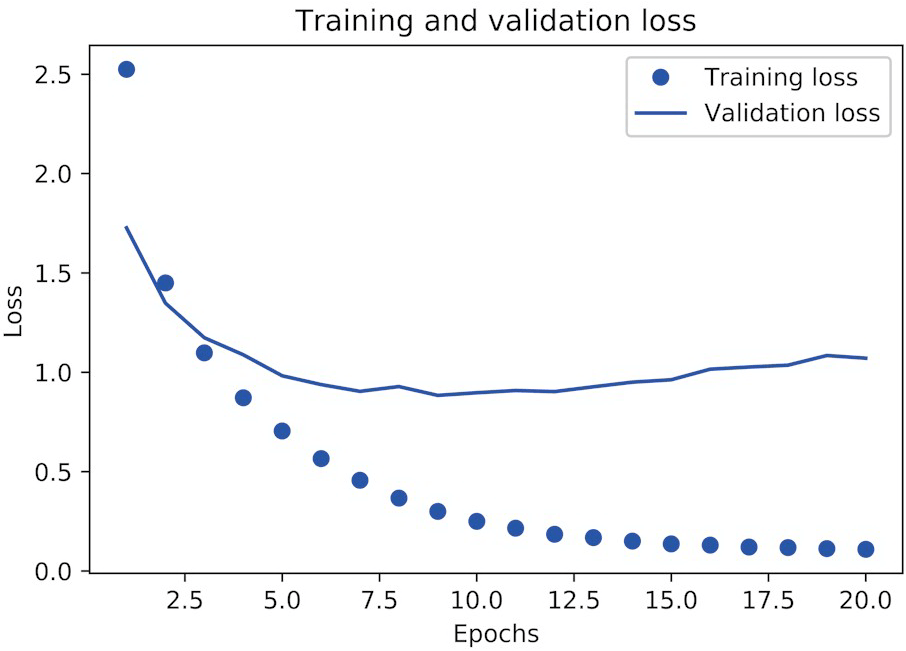
可以看到,训练损失每轮都在降低,训练精度每轮都在提升。但验证损失和验证精度并非如此:它们似乎在第四轮达到最佳值。这就是我们之前警告过的过拟合 (overfit):在第四轮之后对训练数据过度优化,最终学到的表示仅针对于训练数据,无法泛化到训练集之外的数据。为了防止过拟合,我们可以在 3 轮之后停止训练,或者使用一些方法来降低过拟合,我们将在《Keras深度学习笔记(四):机器学习基础》中详细介绍。
我们从头开始训练一个新的网络,训练 4 轮,然后在测试数据上评估模型。
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=4, batch_size=512)
results = model.evaluate(x_test, y_test)
可以看到,这种相当简单的方法就得到了 88% 的精度:
>>> results
[0.2929924130630493, 0.88327999999999995]
使用训练好的网络在新数据上生成预测结果
训练好网络之后,我们希望将其用于实践,可以用 predict 方法来得到评论为正面的可能性大小。
>>> model.predict(x_test)
array([[ 0.98006207]
[ 0.99758697]
[ 0.99975556]
...,
[ 0.82167041]
[ 0.02885115]
[ 0.65371346]], dtype=float32)
可以看到,网络对某些样本的结果非常确信(大于等于 0.99,或小于等于 0.01),但对其他结果却不那么确信(0.6 或 0.4)。
新闻分类:多分类问题
本节我们会构建一个网络,将路透社新闻划分为 46 个互斥的主题。因为有多个类别,所以这是多分类 (multiclass classification) 问题的一个例子。因为每个数据点只能划分到一个类别,所以更具体地说,这是单标签、多分类 (single-label, multiclass classification) 问题。如果每个数据点可以划分到多个类别(主题),那它就是一个多标签、多分类 (multilabel, multiclass classification) 问题。
路透社数据集
路透社数据集包含许多短新闻及其对应的主题,由路透社在 1986 年发布。它是一个简单的、广泛使用的文本分类数据集。它包括 46 个不同的主题,且训练集中每个主题都有至少 10 个样本。
路透社数据集也内置为 Keras 的一部分:
from keras.datasets import reuters
# 加载路透社数据集
(train_data, train_labels), (test_data, test_labels) = reuters.load_data(num_words=10000)
与 IMDB 数据集一样,参数 num_words=10000 将数据限定为前 10,000 个最常出现的单词。我们有 8982 个训练样本和 2246 个测试样本。
>>> len(train_data)
8982
>>> len(test_data)
2246
与 IMDB 评论一样,每个样本都是一个整数列表(表示单词索引):
>>> train_data[10]
[1, 245, 273, 207, 156, 53, 74, 160, 26, 14, 46, 296, 26, 39, 74, 2979,
3554, 14, 46, 4689, 4329, 86, 61, 3499, 4795, 14, 61, 451, 4329, 17, 12]
对应标签是一个 0~45 范围内的整数,即话题索引编号。
>>> train_labels[10]
3
准备数据
可以使用与上一个例子相同的代码将数据向量化。
import numpy as np
from keras.utils.np_utils import to_categorical
def vectorize_sequences(sequences, dimension=10000):
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1.
return results
x_train = vectorize_sequences(train_data) # 将训练数据向量化
x_test = vectorize_sequences(test_data) # 将测试数据向量化
one_hot_train_labels = to_categorical(train_labels) # 将训练标签向量化
one_hot_test_labels = to_categorical(test_labels) # 将测试标签向量化
构建网络
这个主题分类问题与前面的电影评论分类问题类似,但输出类别的数量从 2 个变为 46 个。
Dense 层的堆叠每层只能访问上一层输出的信息,如果某一层丢失了与分类问题相关的一些信息,那么这些信息无法被后面的层找回。上一个例子使用了 16 维的中间层,但对这个例子来说 16 维空间可能太小了,无法学会区分 46 个不同的类别,下面将使用 64 维的层:
from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
注意:
- 最后一层是大小为 46 的
Dense层。对于每个输入样本都会输出一个 46 维向量,这个向量的每个元素(即每个维度)代表不同的输出类别。 - 最后一层使用了
softmax激活。网络将输出在 46 个不同输出类别上的概率分布,其中output[i]是样本属于第 $i$ 个类别的概率。46 个概率的总和为 1。
对于这个例子,最好的损失函数是 categorical_crossentropy (分类交叉熵)。它用于衡量两个概率分布之间的距离,这里分别是网络输出的概率分布和标签的真实分布。通过将这两个分布的距离最小化,训练网络可使输出结果尽可能接近真实标签:
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
验证你的方法
我们在训练数据中留出 1000 个样本作为验证集。
x_val = x_train[:1000]
partial_x_train = x_train[1000:]
y_val = one_hot_train_labels[:1000]
partial_y_train = one_hot_train_labels[1000:]
训练网络,共 20 轮次。
# 训练模型
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))
最后,我们来绘制损失曲线和精度曲线:
import matplotlib.pyplot as plt
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
# 绘制训练损失和验证损失
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plt.clf() # 清空图像
acc = history.history['acc']
val_acc = history.history['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
# 绘制训练精度和验证精度
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
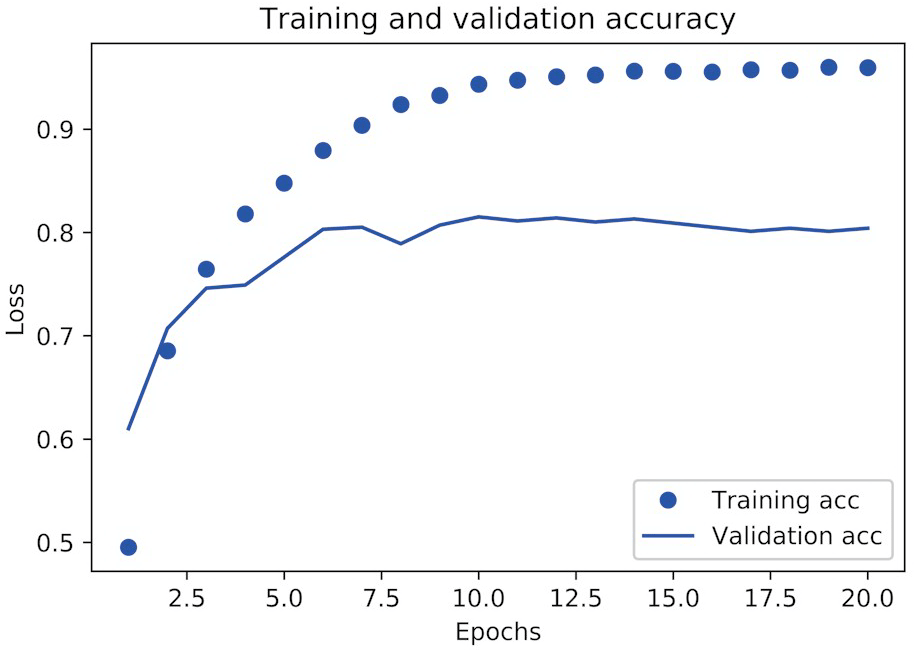
网络在训练 9 轮后开始过拟合。现在我们从头开始训练一个新网络,共 9 个轮次,然后在测试集上评估模型。
# 从头开始重新训练一个模型
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(partial_x_train,
partial_y_train,
epochs=9,
batch_size=512,
validation_data=(x_val, y_val))
results = model.evaluate(x_test, one_hot_test_labels)
这种方法可以得到约 80% 的精度:
>>> results
[0.9565213431445807, 0.79697239536954589]
在新数据上生成预测结果
我们对所有测试数据生成主题预测:
predictions = model.predict(x_test)
predictions 中的每个元素都是长度为 46 的向量。
>>> predictions[0].shape
(46,)
这个向量的所有元素总和为 1:
>>> np.sum(predictions[0])
1.0
最大的元素就是预测类别,即概率最大的类别。
>>> np.argmax(predictions[0])
4
处理标签和损失的另一种方法
前面提到了另一种编码标签的方法,就是将其转换为整数张量,如下所示。
y_train = np.array(train_labels)
y_test = np.array(test_labels)
对于这种编码方法,唯一需要改变的是损失函数的选择。对于整数标签应该使用 sparse_categorical_crossentropy。
model.compile(optimizer='rmsprop',
loss='sparse_categorical_crossentropy',
metrics=['acc'])
这个新的损失函数在数学上与 categorical_crossentropy 完全相同,二者只是接口不同。
中间层维度足够大的重要性
前面提到最终输出是 46 维的,因此中间层的隐藏单元个数不应该比 46 小太多。现在来看一下,如果中间层的维度远远小于 46(比如 4 维),造成了信息瓶颈,那么会发生什么?
# 具有信息瓶颈的模型
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(4, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=128,
validation_data=(x_val, y_val))
现在网络的验证精度最大约为 71%,比前面下降了 8%。导致这一下降的主要原因在于,我们试图将大量信息(这些信息足够恢复 46 个类别的分割超平面)压缩到维度很小的中间空间。网络能够将大部分必要信息塞入这个四维表示中,但并不是全部。
预测房价:回归问题
另一种常见的机器学习问题是回归问题,它预测一个连续值而不是离散的标签。
注意
不要将回归问题与 logistic 回归算法混为一谈。logistic 回归不是回归算法,而是分类算法。
波士顿房价数据集
下面我们预测 20 世纪 70 年代中期波士顿郊区房屋价格的中位数,已知当时郊区的一些数据点,比如犯罪率、当地房产税率等。这个数据集包含的数据点相对较少,只有 506 个,分为 404 个训练样本和 102 个测试样本。输入数据的每个特征(比如犯罪率)都有不同的取值范围。例如,有些特性是比例,取值范围为 0~1;有的取值范围为 1~12;还有的取值范围为 0~100,等等。
# 加载波士顿房价数据
from keras.datasets import boston_housing
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()
我们来看一下数据。
>>> train_data.shape
(404, 13)
>>> test_data.shape
(102, 13)
可以看到,里面有 404 个训练样本和 102 个测试样本,每个样本都有 13 个数值特征,比如人均犯罪率、每个住宅的平均房间数、高速公路可达性等。
目标是房屋价格的中位数,单位是千美元。
>>> train_targets
array([ 15.2, 42.3, 50. ... 19.4, 19.4, 29.1])
准备数据
将取值范围差异很大的数据输入到神经网络中是有问题的,网络可能会自动适应这种取值范围不同的数据,但学习肯定变得更加困难。对于这种数据,普遍采用的最佳实践是对每个特征做标准化,即对于输入数据的每个特征(输入数据矩阵中的列),减去特征平均值,再除以标准差,这样得到的特征平均值为 0,标准差为 1。用 Numpy 可以很容易实现标准化。
# 数据标准化
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
test_data -= mean
test_data /= std
注意,用于测试数据标准化的均值和标准差都是在训练数据上计算得到的。在工作流程中,我们不能使用在测试数据上计算得到的任何结果,即使是像数据标准化这么简单的事情也不行。
构建网络
由于样本数量很少,我们将使用一个非常小的网络,其中包含两个隐藏层,每层有 64 个单元。一般来说,训练数据越少,过拟合会越严重,而较小的网络可以降低过拟合。
from keras import models
from keras import layers
# 模型定义
def build_model(): # 因为需要将同一个模型多次实例化,所以用一个函数来构建模型
model = models.Sequential()
model.add(layers.Dense(64, activation='relu',
input_shape=(train_data.shape[1],)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(1))
model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
return model
网络的最后一层只有一个单元,没有激活,是一个线性层。这是标量回归(标量回归是预测单一连续值的回归)的典型设置。
注意,编译网络用的是 mse 损失函数,即均方误差 (MSE,mean squared error),预测值与目标值之差的平方。这是回归问题常用的损失函数。
在训练过程中还监控一个新指标:平均绝对误差 (MAE,mean absolute error)。它是预测值与目标值之差的绝对值。比如,如果这个问题的 MAE 等于 0.5,就表示你预测的房价与实际价格平均相差 500 美元。
利用 K 折验证来验证你的方法
为了在调节网络参数(比如训练的轮数)的同时对网络进行评估,我们可以将数据划分为训练集和验证集。但由于数据点很少,验证集会非常小。因此,验证分数可能会有很大波动,也就是说,验证集的划分方式可能会造成验证分数上有很大的方差,这样就无法对模型进行可靠的评估。
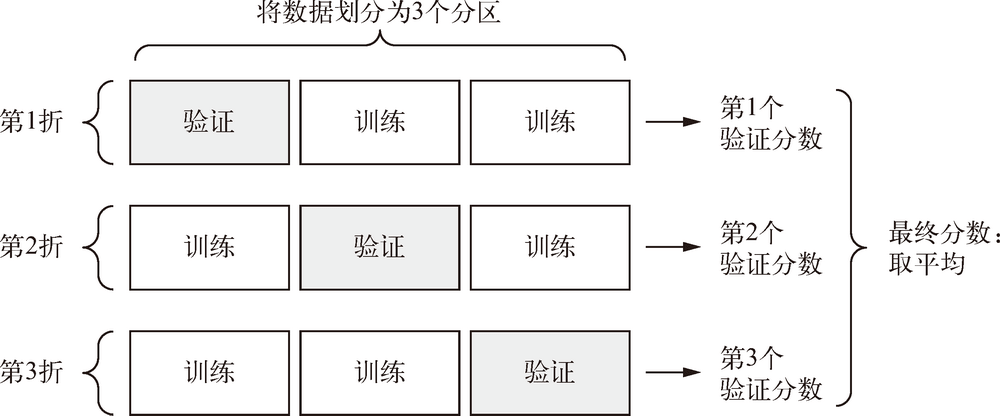
在这种情况下,最佳做法是使用 K 折交叉验证。这种方法将可用数据划分为 K 个分区(K 通常取 4 或 5),实例化 K 个相同的模型,将每个模型在 K - 1 个分区上训练,并在剩下的一个分区上进行评估。模型的验证分数等于 K 个验证分数的平均值。下图展示了 3 折交叉验证:
这种方法的代码实现很简单:
# K 折验证
import numpy as np
k = 4
num_val_samples = len(train_data) // k
num_epochs = 100
all_scores = []
for i in range(k):
print('processing fold #', i)
# 准备验证数据:第k个分区的数据
val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
# 准备训练数据:其他所有分区的数据
partial_train_data = np.concatenate(
[train_data[:i * num_val_samples],
train_data[(i + 1) * num_val_samples:]],
axis=0)
partial_train_targets = np.concatenate(
[train_targets[:i * num_val_samples],
train_targets[(i + 1) * num_val_samples:]],
axis=0)
# 构建Keras模型(已编译)
model = build_model()
# 训练模型(静默模式,verbose=0)
model.fit(partial_train_data, partial_train_targets,
epochs=num_epochs, batch_size=1, verbose=0)
# 在验证数据上评估模型
val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)
all_scores.append(val_mae)
设置 num_epochs = 100,运行结果如下。
>>> all_scores
[2.588258957792037, 3.1289568449719116, 3.1856116051248984, 3.0763342615401386]
>>> np.mean(all_scores)
2.9947904173572462
每次运行模型得到的验证分数有很大差异,从 2.6 到 3.2 不等。平均分数 3.0 是比单一分数更可靠的指标——这就是 K 折交叉验证的关键。在这个例子中,预测的房价与实际价格平均相差 3000 美元,考虑到实际价格范围在 10,000~50,000 美元,这一差别还是很大的。
我们让训练时间更长一点,达到 500 个轮次。为了记录模型在每轮的表现,我们需要修改训练循环,以保存每轮的验证分数记录。
num_epochs = 500
all_mae_histories = []
for i in range(k):
print('processing fold #', i)
# 准备验证数据:第k个分区的数据
val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
# 准备训练数据:其他所有分区的数据
partial_train_data = np.concatenate(
[train_data[:i * num_val_samples],
train_data[(i + 1) * num_val_samples:]],
axis=0)
partial_train_targets = np.concatenate(
[train_targets[:i * num_val_samples],
train_targets[(i + 1) * num_val_samples:]],
axis=0)
# 构建Keras模型(已编译)
model = build_model()
# 训练模型(静默模式,verbose=0)
history = model.fit(partial_train_data, partial_train_targets,
validation_data=(val_data, val_targets),
epochs=num_epochs, batch_size=1, verbose=0)
mae_history = history.history['val_mean_absolute_error']
all_mae_histories.append(mae_history)
然后我们可以计算每个轮次中所有折 MAE 的平均值。
# 计算所有轮次中的 K 折验证分数平均值
average_mae_history = [
np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]
我们画图来看一下:
import matplotlib.pyplot as plt
# 绘制验证分数
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()
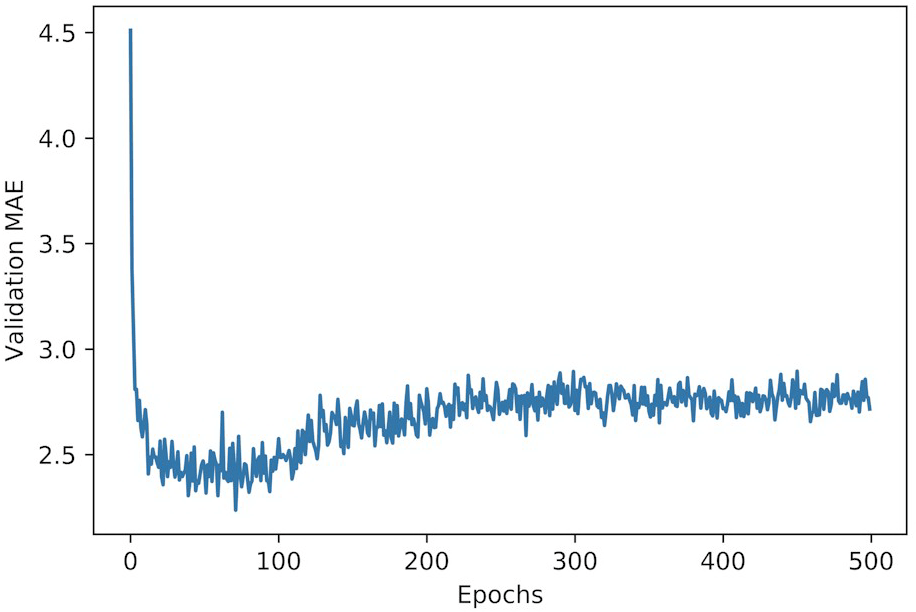
因为纵轴的范围较大,且数据方差相对较大,所以难以看清这张图的规律。我们来重新绘制一张图。
- 删除前 10 个数据点,因为它们的取值范围与曲线上的其他点不同。
- 将每个数据点替换为前面数据点的指数移动平均值,以得到光滑的曲线。
def smooth_curve(points, factor=0.9):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous * factor + point * (1 - factor))
else:
smoothed_points.append(point)
return smoothed_points
smooth_mae_history = smooth_curve(average_mae_history[10:])
plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()
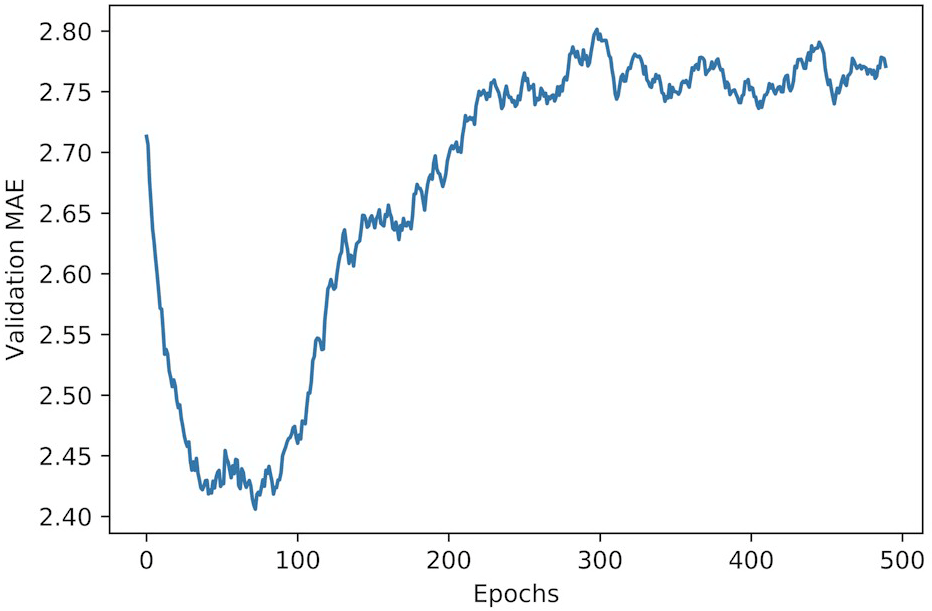
从图上可以看出,验证 MAE 在 80 轮后不再显著降低,之后就开始过拟合。
完成模型调参之后(除了轮数,还可以调节隐藏层大小),你可以使用最佳参数在所有训练数据上训练最终的生产模型,然后观察模型在测试集上的性能。
# 训练最终模型
model = build_model() # 一个全新的编译好的模型
model.fit(train_data, train_targets, # 在所有训练数据上训练模型
epochs=80, batch_size=16, verbose=0)
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)
最终结果如下:
>>> test_mae_score
2.5532484335057877
我们预测的房价还是和实际价格相差约 2550 美元。
总结
- 通常需要对原始数据进行大量预处理,以便将其转换为张量输入到神经网络中。单词序列可以编码为二进制向量,但也有其他编码方式。
- 带有
relu激活的Dense层堆叠,可以解决很多种问题。 - 对于二分类问题,网络的最后一层应该是只有一个单元并使用
sigmoid激活的Dense层,网络输出应该是 0~1 范围内的标量,表示概率值,损失函数应该使用binary_crossentropy。 - 无论你的问题是什么,
rmsprop优化器通常都是足够好的选择。 - 随着神经网络在训练数据上的表现越来越好,模型最终会过拟合,并在前所未见的数据上得到越来越差的结果。一定要一直监控模型在训练集之外的数据上的性能。
- 如果要对 N 个类别的数据点进行分类,网络的最后一层应该是大小为 N 的
Dense层。 - 对于单标签、多分类问题,网络的最后一层应该使用
softmax激活,这样可以输出在 N 个输出类别上的概率分布。损失函数几乎总是应该使用分类交叉熵。它将网络输出的概率分布与目标的真实分布之间的距离最小化。 - 处理多分类问题的标签有两种方法。
- 通过分类编码(也叫 one-hot 编码)对标签进行编码,然后使用
categorical_crossentropy作为损失函数。 - 将标签编码为整数,然后使用
sparse_categorical_crossentropy损失函数。
- 通过分类编码(也叫 one-hot 编码)对标签进行编码,然后使用
- 如果你需要将数据划分到许多类别中,应该避免使用太小的中间层,以免在网络中造成信息瓶颈。
- 回归问题使用的损失函数与分类问题不同。回归常用的损失函数是均方误差 (MSE)。使用的评估指标也与分类问题不同(精度的概念不适用于回归问题),常见的回归指标是平均绝对误差(MAE)。
- 如果输入数据的特征具有不同的取值范围,应该先进行预处理,对每个特征单独进行缩放。
- 如果可用的数据很少,使用 K 折验证可以可靠地评估模型。
- 如果可用的训练数据很少,最好使用隐藏层较少(通常只有一到两个)的小型网络,以避免严重的过拟合。
该文是《Python深度学习》的阅读笔记,内容摘自原书,部分内容有修改。